Амплитуда гармонических колебаний

1. Собственные электрические колебания
2. Идеальный электрический контур
3. Гармонические механические колебания

Колебания имеют огромное значение в различных механических процессах. Такие процессы повторяются во времени с определенным периодом и частотой. К примеру, движения планет солнечной системы, движение машин и механизмов, стрелки часов, различные звуки имеют определенную частоту колебаний.

Если рассмотреть электромагнитные явления, то их основу так же составляют электромагнитные колебания, здесь все параметры изменяются по законам периодичности.

Данные колебания используются в разнообразных устройствах, телефонии, телеграфии, радиосвязи, в переменных токах, освещении.

Собственные колебания - это колебания, происходящие в результате действия внутренних сил в системе. Эти колебания возникают при нарушении равновесного состояния в колебательной системе.

Гармонические колебания – это такие колебания, которые можно описать с помощью закона синуса или косинуса.

Собственные электрические колебания

Если электрический процесс в контуре из конденсатора (емкостью С), сопротивления (R) и катушки индуктивности (L) является квазистационарным, то это значит, что в каждой точке контура мгновенная сила тока (I) будет одинаковой и для мгновенных значений электрических параметров будут применяться законы Кирхгофа.

В контуре такого вида изменение зарядов будет описываться дифференциальным уравнением второго порядка с обычными производными и постоянными коэффициентами. Это уравнение такого вида:

\({b^2a\over dt^2}+2a{dq\over dt}+ω_0^2q=0 (1),\)

где \(ω_0={1\over LC}\) – циклическая (круговая) частота колебаний, \(a={R\over 2L},\)

Такие же уравнения используют для описания процессов колебаний силы тока и напряжения.

Колебания, описывающиеся дифференциальными линейными уравнениями, называются линейные, а системы с такими колебаниями называются линейные колебательные системы.

Не нашли то, что искали?

Попробуйте обратиться за помощью к преподавателям

Тип работы Выберите тип работыКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Идеальный электрический контур

Для полного определения задачи описания колебаний должны быть заданы два начальных условия для уравнения второго порядка. Зачастую начальные условия для уравнения задаются в таком виде:

\(q=q_0,\)  при  \(t=0;\)

\({dq\over dt}=0.\)

При сопротивлении контура, равном нулю \((R = 0)\), уравнение запишется таким образом:

\({d^2q\over dt^2}+ω_0^2q=0 (2),\)

Общее решение этого уравнения будет гармоническим колебанием:

\(q=Acos(ω_0 t+φ)(3),\)

где \(A\) – амплитуда колебаний;  \(φ\) – начальная фаза колебаний.

Если подставить начальное условие \(Acosφ=q_0\) в формулу, то она запишется как: \(Aω_0sinφ=0 (4)\)).

Из чего следует, что \(φ=0, (4)A=q_0\)

Напряжение конденсатора контура описывается таким уравнением: \(U_c={q\over c}=U_0 cosω_0t (5),\)

где амплитуда напряжения равняется начальному напряжению конденсатора  \(U_0={q_0\over c}.\)

Сила тока контура определяется уравнением \(I=-{sq\over dt}=q_0ω_0sin (ωt)=I_0sin (ω_0t) (6),\)

где \(I_0=q_0ω_0\) – амплитуда силы тока.

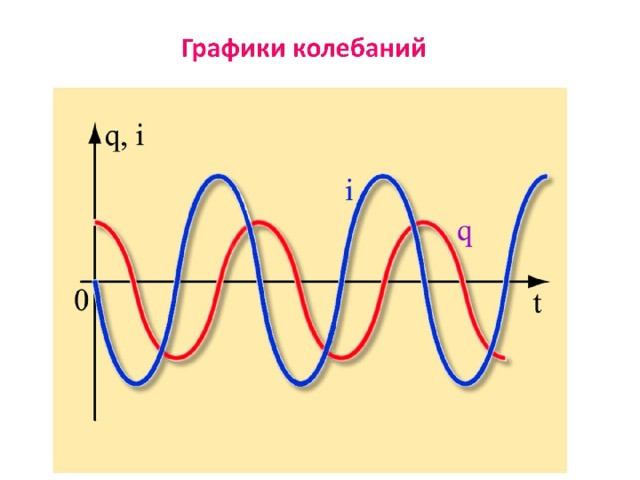
Если сравнить уравнения (4) и (6), то можно сделать вывод, что изменения заряда и силы тока происходят согласно гармоническим законам: заряд колеблется в соответствии с законом косинуса, а сила тока – в соответствии с законом синуса.

В тригонометрии известна зависимость \(sinω_0t=cos(ω_0t-{π\over 2})​​\), то есть разница фаз \({π\over 2}\) есть между колебанием силы тока и заряда, причем сила тока отстает по фазе.

Если графически изобразить колебания вдоль горизонтальной оси времени, при этом в качестве вертикали будет сила тока, заряд или напряжение, то кривая будет в виде синусоиды или косинусоиды. Форма этой кривой будет зависеть амплитуды колебаний физического параметра и циклической частоты \(ω_0\). Расположение будет зависеть от первоначальной фазы.

Сложно разобраться самому?

Попробуйте обратиться за помощью к преподавателям

Тип задания Выберите тип заданияКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Гармонические механические колебания

Уравнение координаты для гармонических колебаний материальной точки, совершающей движения вдоль оси \(X\) будет выглядеть следующим образом:

\(x=Acos(ωt⁡+δ) (7)\) (7),

где \(δ\) – начальная фаза колебаний,

\(A\) – амплитуда колебаний,

\(ω\) – циклическая частота колебаний.

Для определения скорости колебаний материальной точки вдоль оси \(X\) используют уравнение следующего вида: \(v=-ωAsin(ωt⁡+δ) (8).\).

Амплитуда ускорения материальной точки при этом будет равняться \(a_m=-ω^2A .\)

Явление затухания колебаний

Рассмотрим теперь реальный электрический контур, который имеет определенное сопротивление. Здесь колебания будут происходить по закону, который описывается уравнением (1).

При этом, если \( ω_0^2  >α^2\), то решение этого уравнения будет выглядеть так:

\(q=Ae^{-αt}cos(ωt⁡+δ) (9)\),

где \(A\) и \(φ\) – постоянные величины, которые задаются изначально,

\(ω=\sqrt{ω_0^2-α^2}\).

Соответственно это уравнение описывает гармоническое колебание с циклической частотой \(ω\) и амплитудой, которая равна: \(y=Ae^{-αt} (10)\), которая постоянно уменьшается со временем, то есть не есть постоянной, а затухает.

При этом \(α\) – это коэффициент затухания.