Учебные материалы
для студентов и школьников

Геометрия механического движения. Равномерное движение по окружности

1. При движении объект описывает какую-то траекторию
2. Эллиптическое движение
3. Параболическое движение
4. Гиперболическое движение
5. Движение по окружности

При движении объект описывает какую-то траекторию.

Определение 1

Механическим движением является изменение местоположения объекта в пространстве по отношению к другим объектам. Такое изменение занимает определенное время. Взаимодействия движущихся тел описывают классическими законами механики.

В зависимости от геометрических особенностей протекания процесса различают несколько видов механического движения:

гиперболическое;
параболическое;
по окружности;
эллипсоидное;
по кривой погони;
по кривой ускоренного спуска;
по квадратрисе.

Эллиптическое движение

При таком движении траектория объекта представлена геометрической фигурой – эллипсом.

Определение 2

Эллипсом есть замкнутая кривая в плоскости, сумма расстояний от каждой точки которой до двух точек F_1и F_2 является постоянной величиной.

Контрольными точками, по которым рассчитываются расстояния эллипса, есть его фокусы F_1и F_2. Эллипс получается из окружности в результате аффинного преобразования ортогональной проекции окружности на плоскость.

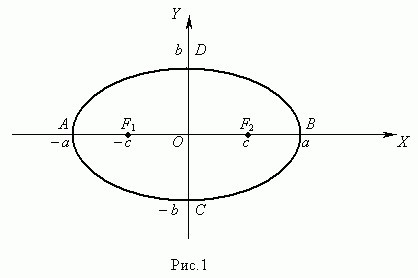
Малой осью эллипса есть отрезок $b+b$, перпендикулярный большой оси эллипса $a+a$ и проходящий через его центр $O$, а концами лежащий на эллипсе.

Не нашли то, что искали?

Попробуйте обратиться за помощью к преподавателям

Тип работы

Предмет

E-mail

это быстро и бесплатно

Центр эллипса – это точка пересечения его большой и малой осей. Отрезки $a$ и $b$ – это большие и малые полуоси эллипса. Они начинаются от его центра и заканчиваются в вершинах осей.

Замечание 1

Фокальные радиусы – это расстояния от фокусов эллипса до его точек. Обозначаются буквами $r_1$ и $r_2$.

Произвольная хорда, проведенная через центр эллипса, есть его диаметром.
Радиусом эллипса в точке считается отрезок, что соединяет его центр с заданной точкой.

Отрезок, опущенный с фокуса на эллипс и перпендикулярный его большой оси, является фокальным параметром и определяется таким образом:
$p={b^2\over a}.$

Параболическое движение`.`

Определение 3

Параболой является кривая в плоскости, точки которой равноудалены от заданной прямой и определенной точки.

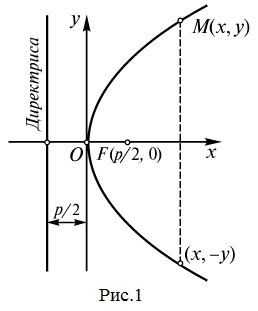
Классическое уравнение параболы, что задана в прямоугольной системе координат, выглядит следующим образом:

$y^2=2px, p>0,$

где $p$ – фокальный параметр.

Фокальный параметр показывает расстояние между директрисой и фокусом. Поскольку каждая точка параболы равноудалена от директрисы и фокуса, то ее вершина будет находиться на середине фокального параметра ${p\over 2}.$

Таким образом, уравнение параболы будет представлено квадратичной функцией:

$y=ax^2+bx+c$, при $a≠0$.

Общее уравнение параболы выглядит так:

$Ax^2+Bxy+Cy^2+Dx+Ey+F=0.$

Физики оперируют понятием второй космической скорости, при которой под воздействием гравитационного поля тела описывают параболическую траекторию движения. Эту скорость также называют параболической. При развитии данной скорости тело преодолевает силу тяготения Земли и попадает в космос. То есть, это та скорость, которая необходима телу для выхода из гравитационного поля планеты.
Данную скорость рассчитывают из закона сохранения энергии:

${\frac {mv_{2}^{2}}{2}}-G{\frac {mM}{R}} = 0$

где $m$ – масса тела;
$v_2$ – вторая космическая скорость;
$G$ – гравитационная постоянная;
$M$ – масса Земли;
$R$ – расстояние от центра Земли до тела.
Таким образом, вторую космическую скорость определяют так:

$v_{2} = {\sqrt {2G{\frac {M}{R}}}}$.

Гиперболическое движение

Определение 4

Гиперболой является кривая в плоскости, для всех точек которой является постоянной абсолютная разность расстояний между одной и двумя конкретными точками.

${\bigl |}|F_{1}M|-|F_{2}M|{\bigr |} = 2a$, где $|F_{1}F_{2}|>2a>0$.

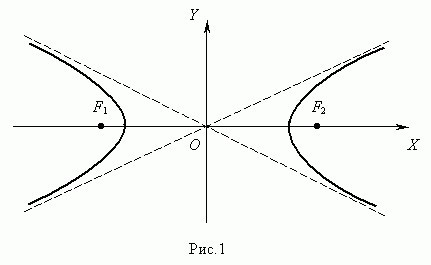
Гипербола представляет собой квадрику и сечение конуса.
Равнобочная гипербола – это такая, у которой $a=b$. Для прямоугольной системы координат уравнение гиперболы имеет следующий вид:

$xy=a^2$.

Движение по окружности

Замечание 2

Равномерное движение по окружности считается одним из простых примеров движения по кривой.

Сложно разобраться самому?

Попробуйте обратиться за помощью к преподавателям

Тип задания

Предмет

E-mail

это быстро и бесплатно

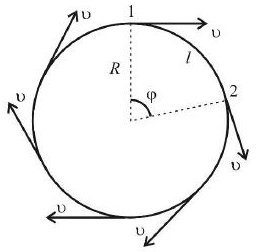
Скорость движения объекта по окружности выражается линейной скоростью, модуль которой для равномерного движения остается постоянным:

$v=const$.

Меняется лишь вектор направления скорости.

Центростремительным ускорением есть величина, показывающая изменение вектора скорости в направлении, в котором исключено тангенциальное ускорение. Модуль центростремительного ускорения рассчитывается следующим образом:

$a={v^2\over R}$,

где $a$ – центростремительное ускорение;
$v$ – линейная скорость;
$R$ – радиус окружности.

Для характеристики движения объекта по окружности используют величину угла поворота радиуса. Это угол, на который за определенное время поворачивается радиус, проведенный от центра окружности к точке расположения объекта. Измеряется в радианах (рад).

$φ={l\over R}$,

где $φ $– угол поворота радиуса;
$ l$ – длина окружности.

$l=2πR$.

Еще одним параметром, описывающим движение тела по окружности, считается угловая скорость равномерного движения $ω$ (рад/с). Она рассчитывается по такой формуле:

$ω={φ\over t}$,

где $t$ – время, за которое совершен поворот.

Линейная скорость равномерного движения определяется таким образом:

$v={2πR\over T}=2πRν$,

где $T$ – период;
$ν$ – частота.

Не нашли нужную информацию?

Закажите подходящий материал на нашем сервисе. Разместите задание – система его автоматически разошлет в течение 59 секунд. Выберите подходящего эксперта, и он избавит вас от хлопот с учёбой.

Все работы выполняются без посредников, поэтому цены вас приятно удивят.

В рамках задания они бесплатны и выполняются в оговоренные сроки.

Если эксперт не справился – гарантируем 100% возврат средств.

Наши менеджеры работают в выходные и праздники, чтобы оперативно отвечать на ваши вопросы.

Мы отбираем только надёжных исполнителей – профессионалов в своей области. Все они имеют высшее образование с оценками в дипломе «хорошо» и «отлично».

1 000 +

Новых заказов каждый день