Неравновесная термодинамика

1. Представление неравновесной термодинамики
2. Деятельность термодинамики неравновесных явлений
3. Принцип локального равновесия

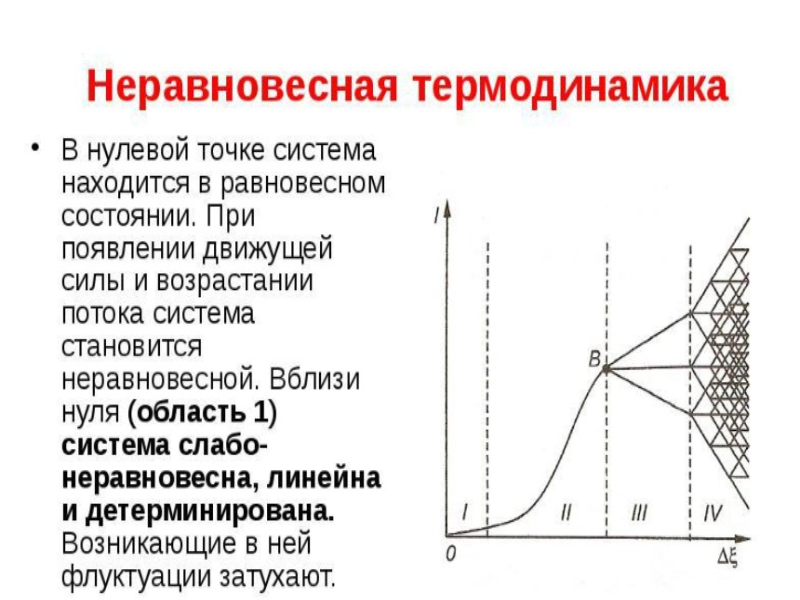
Рисунок 1. Неравновесная термодинамика.

В нулевой точке, система располагается в состоянии равновесия. При появлении движущей силы и увеличении потока, она становится неравновесной. Поблизости нуля (область I) система слабо неравновесная, линейна и детерминирована. Возникающие в системе флуктуации затухают.

Появление этой сферы познания взаимно связано, прежде всего, с тем фактором, что большое количество существующих систем в окружающем мире находятся довольно в далеком от состояния термодинамического равновесия.

Представление неравновесной термодинамики

Иначе говоря, рассматриваемую систему возможно умозрительно разделить на огромное количество элементарных групп, которые в то же время так велики, что их исследование будет возможно в виде макроскопических систем, однако, вместе с этим, такие маленькие, чтоб состояние любой из этих систем подходило к равновесному состоянию.

Аналогичное соображение будет правильным в интересах довольно большого класса материальных систем, и это является устанавливающим фактором результата с точки зрения традиционного описания неравновесной термодинамики, в пределах которой формулировка необратимых явлений будет реализуема, с помощью ввода в действие сил и потоков термодинамики.

Сложно разобраться самому?

Попробуйте обратиться за помощью к преподавателям

Тип задания Выберите тип заданияКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Основой для ввода этих значений считается то, что через них формирование энтропии проявляется в простейшем виде. Важнейшим итогом, который получен в пределах линейной неравновесной термодинамики, считается теорема о минимальном формировании энтропии. В среде линейного порядка, абсолютное формирование энтропии в системе, которая подвергается потоку энергии и вещества, досягает в постоянном неравновесном состоянии собственного минимума.

Невзирая на достижения традиционного подхода, у него существуют существенный недостаток, который базируется на варианте локального равновесия, что, в то же время, может трансформироваться в сильно серьезное предположение для довольно широкого класса явлений и систем. Для форсирования данной ситуации, в физике разработаны конкретные разнообразные подходы. Образцами являются следующие процессы:

• Расширение ультразвуковых волн в газообразных веществах.
• Смесь жидкости либо газа с твердыми элементами.
• Неплотные газообразные вещества.
• Ударные волны.

Деятельность термодинамики неравновесных явлений

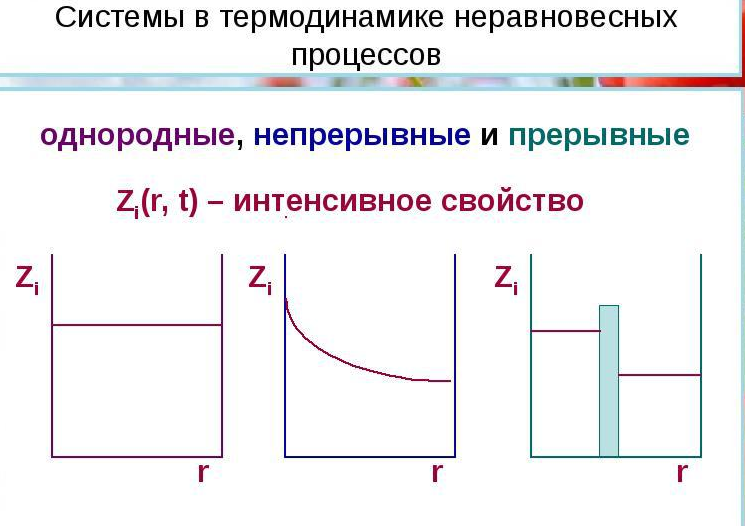
Рисунок 2. Системы в термодинамике неравновесных явлений.

Выделяют теорию и феноменологическую термодинамику неравновесных явлений, которая подразделяется на нелинейную и линейную теории. Типичным образом в термодинамике неравновесных явлений предметом интереса исследователей является 3 вида систем:

• Однородные системы. В данных системах в определенный промежуток времени интенсивные характеристики будут равнозначными по всему объему.
• Непрерывные системы. В данных системах характеристики могут являться непрерывными функциями положения точки в системе и времени. Это полевые переменные.
• Прерывные системы. Данные системы состоят из более двух однотипных компонентов, поделенных либо границами раздела фаз, либо вентилем. Например, газообразные вещества в емкостях, которые соединены мембраной. Следовательно, характеристики меняются благодаря скачку во время перемещения из одного компонента в иной.

Соответствия, характеризующие явления перехода энергии, массы, заряда, энтропии и прочее, фиксируются как балансные формулы, применяемые для двух видов систем: непрерывных и прерывных. В данных системах постоянно будут участвовать значения двух видов. Один вид рассматривается как поток, а второй вид рассматривается как сила. Потоки квалифицируют скорость перехода материальной величины через предполагаемую одиночную площадь.

Неравновесные явления разделены в соответствии от разновидностей потоков силы:

• Скалярные процессы (скаляры).
• Тензорные процессы (тензоры).
• Векторные процессы (векторы).

В зависимости от этого, с целью изображения явлений необходимо использовать соответственный тип поля.

К категории скалярных явлений возможно причислить химические реакции. К примеру, скорость реакции в системе во всех ее координатах квалифицируется скалярным значением.

К категории векторных явлений возможно причислить диффузию и тепловую проводимость. У данных параметров существует взаимосвязь с полями векторов потоков вещества и теплоты.

В роли естественного образца тензорного явления считается вязкое течение.

Принцип локального равновесия

Рисунок 3. Неравновесная термодинамика.

В нелинейной термодинамике неравновесных явлений важнейшим считается принцип локального равновесия. Балансные формулы создаются аналогично, подобным образом линейной термодинамике неравновесных явлений, однако, в то же время, взаимосвязи меж потоками и силами будет характерна нелинейная природа.

В роли классического образца могут являться химические реакции. Это поясняет особенную ценность и значимость нелинейной термодинамики неравновесных явлений для биолого-химических систем. Функционирование систем в условиях нелинейного окружения имеет некоторое количество фундаментальных различий, по сравнению с окружением взаимодействия линейных соответствий.

Не нашли то, что искали?

Попробуйте обратиться за помощью к преподавателям

Тип работы Выберите тип работыКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Таким образом, первое, в границах системы лишаются собственной достоверности соответствия взаимности Онзагера, появляется анизотропия свойств, даже при условии изотропности системы в состоянии равновесия.

Второе, одновременно с тем как постоянные и равновесные состояния возле равновесного изображаются в тождествах конкретных термодинамических потенциалов, в сферах, очень далеких от него, обнаружить данные потенциалы не выходит.

Третье, когда поблизости состояния равновесия представление в термодинамике систем производится чрез вероятные усредненные материальные значения, а флуктуации допускают характеристику внезапным погрешностям от усредненных, в отдалении от равновесия флуктуации начинают устанавливать усредненную величину.