






Зачастую только вспоминания о дифференциальных уравнениях (ДУ, дифур) приводит учащихся в паническое состояние. Это происходит по причине, что есть некоторые пробелы в изучении материалов. И последующее изучение ДУ кажется непреодолимым. Сделаем попытку продемонстрировать, что дифференциальные уравнения считаются не настолько сложными, как может представляться первоначально.
Со школьных времен все знают о простых уравнениях, где требуется рассчитать неизвестную переменную. В принципе ДУ только немного различаются с такими уравнениями. На место неизвестной переменной требуется поставить функцию y(х), и рассчитать данное уравнение. Решить диферренциальное уравнение - это значит найти множество функций, удовлетворяющих заданному уравнению.
ДУ обладает большим предназначением на практике. Он является не математической абстракцией, не имеющей отношения к нашему окружению. Благодаря дифференциальным уравнениям объясняется большая часть реалистичных процессов в природе. К примеру решения ДУ, возможно отнести: колебания струны, расчет скорости, а также ускорения у различных объектов. В том числе, ДУ довольно широко применяются в физике, химии, в экономических науках, а также в иных научных деятельностях.
Дифференциальное уравнение считается уравнением, содержащим производные функции y(х), непосредственно функцию, разные переменные в разнообразных сочетаниях. Есть огромное количество ДУ:
Решением дифуров считается функция, обращающая это ДУ в равенство. Присутствуют общие примеры решения, предоставляющее огромное множество вариантов, как решать ДУ, а также частные решения дифуров, удовлетворяющие условиям первоначально указанным. Общий порядок ДУ устанавливается наивысшим порядком производных, которые в него входят.
Обыкновенные ДУ являются уравнениями, которые имеют одну переменную. Произведем рассмотрение простого обычного дифура первого порядка. Данное ДУ обладает таким видом:
\(y'(x)=f(x) \)
Справиться с расчетами данного ДУ возможно, просто осуществит интегрирование f (x). Примеры решения таких дифференциальных уравнений:
\(y'(x)=0 \)
\(y'(x)=x+e^x-1\)
Общий вид данных дифуров:
\(y'(x)=f(x) g(y)\)
Например,
\(2x = \sqrt{1-y^2} =y'(1+x^2)\)
Производя решение такого дифференциального уравнения, необходимо произвести разделение переменных, осуществив его приведения к виду:
\({ y'(x) \over g(y)}=f(x)\)
А далее, осуществить интегрирование обеих сторон уравнения.
Линейные дифференциальные уравнения обладают таким видом:
\(y'+p(x)y=q(x)\)
В данном дифуре, p(x) и q(x) считаются функциями свободной переменной. В свою очередь, y = y(x) считается функцией, подлежащей нахождению. Одним из образцов такого уравнения считается следующее равенство:
\(y'={ 2xy \over 1+x}=1+x^2\)
Осуществляя решение ДУ, зачастую применяют метод модификации свободной константы. Но возможно показывать функцию, подлежащую нахождению, как произведения двух других функций \(y(x) = u(x)*v(x).\)
Решаем ДУ с установленными первоначальными параметрами.
\(x^2yy''=(y-xy')^2\)
Пример решения.
Осуществим работу по проверке, возможно ли считать это ДУ однородным по отношению к функции и к производным этой функции
\(y \to ty, y'\to ty', y''\to ty'':\)
\(x^2tytyy''=(ty-xty')^2=t^2(y-xy')^2;\)
Либо
\(t^2x^2yy''=t^2(y-xy')^2,\)
Сокращение переменной t говорит, что данное уравнение однородное.
Подставляем:
\(y' = uy.\)
После этого:
\(y'' = (y')'=(uy)'=u'y+uy'=u'y+uuy=y(u'+u^2)\)
Осуществляем подстановку в первоначальное ДУ:
\(x^2yy(u'+u^2)=(y-xuy)^2=y^2(1-xu)^2.\)
\(x^2(u'+u^2)=(1-xu)^2=1-2xu+x^2u^2;\)
\(x^2u'=x^2u^2=1-2xu+x^2u^2;\)
\(x^2u'=1-2xu;\)
\(x^2u'+2xu=1;\)
Данное линейное ДУ считается 1 порядка. И его возможно решить благодаря интегрирующему множителю, равному 1:
\(x^2u'+2xu=x^2u'+(x^2)'u={ d(x^2u)\over dx}=1.\)
В результате получим:
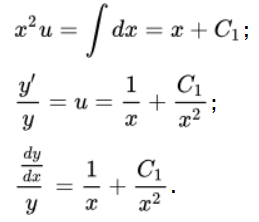
Осуществляем умножение на dx и производим преобразования с помощью интегрирования:
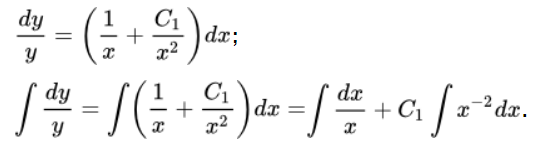
Интегральные части являются табличными:
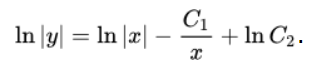
Выполняем потенцирование.
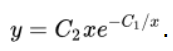
Осуществляем замену коэффициентов \(C_1\) на \(C_1.\)
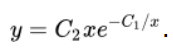
Осуществить решение задачи Коши для ДУ 2-го порядка.
\(2yy''+1=(y')2, y(1/3)=1, y'(1/3)=2.\)
Решение задания: заменим производную второго порядка \(y''\)
\(y'=p,y''-p'={ dp \over dy}{ dy \over dx}={ dp \over dy}p,\)
ДУ будет иметь следующую форму
\(2yp{ dp \over dy}+1=p^2\)
Это дает возможность получения ДУ с разделяющимися переменными.
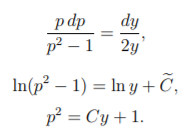
Рассчитаем значение коэффициента C из первоначального задания \((4 – 1 = 1, C = 3)\)
Следовательно, \(p = \sqrt{3y+1} \)
Осуществим возвращение к первоначальным данным \((p = y').\)
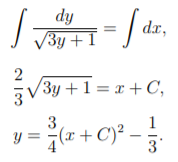
Рассчитаем постоянной из первоначального задания:
\((3/4(1/3+C)^2-1/3=1,\implies C=1).\)
Расчет задачи Коши:
\(y(x)=3/4(x+1)^2-1/3.\)
Не нашли то, что искали?
Попробуйте обратиться за помощью к преподавателям
ДУ с постоянными параметрами обладает следующей формой:
\(a_ny^{(n)}+ \dotsm +a_2y''+a_1y'+a_0y=0.\)
В данном ДУ am считаются действительными значениями. Для вычисления всеобщего решения данного дифура требуется вычислить n линейных решений, которые считаются независимыми.
\(y_i(x), \left\{i=1,2,3,...,n \right\},\)
Данные линейные разрешения основывают основополагающую систему вычислений. После чего, всеобщее вычисление устанавливается соответственно уравнению:
\(y=C_1y_1(x)+C_2y_2(x)+ \dotsm +C_ny_b(x).\)
Находим решение в следующей форме: \(y = e^{(kx)}\) Осуществляем получение характерной формулы.
\(a_nk^n+a_{n-1}k^{n-)}+ \dotsm +a -2k^2+a_1k+a_0=0.\)
Когда данное уравнение обладает разными корнями
\(k_m, \left\{m=1,2,3,...,n \right\},\)
тогда основополагающая система вычислений обладает таким выражением:
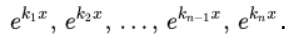
Когда присутствует совокупный корень
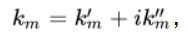
Тогда присутствует совокупно сопряженный корень.
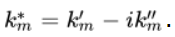
Подобным корням отвечают следующие решения:
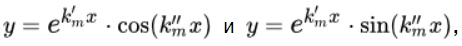
Данные решения будут включены в основополагающую систему вычислений, заменяя совокупные решения
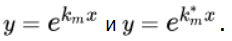
Кратным корням \(k_m = k_{m+1} = … = k_{m+r-1}\) кратности r отвечают линейные решения, которые независимы.
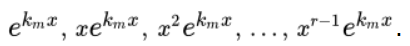
Кратным совокупным корням
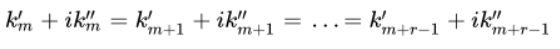
Кратности r и их совокупно связанным величинам отвечают 2r линейные решения дифференциального уравнения, которые независимы.
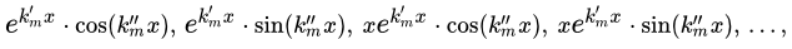
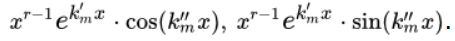
Выполнить работу по решению дифференциального простого линейного уравнения в частных производных 1-го порядка разрешить задачу Коши с определенным предельным заданием:
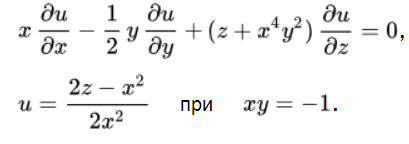
Пример решения.
Выстраиваем дифференциальное уравнение свойств:
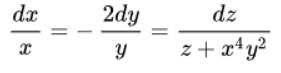
Данное ДУ свойств состоит из 3-х уравнений:
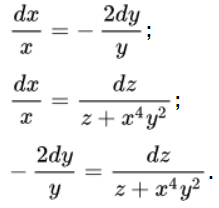
Требуется решение двух уравнений, а третье будет решено, само собой.
Осуществляем решение первого уравнения:
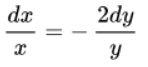
Осуществлено разделение переменных. Далее будем интегрировать:
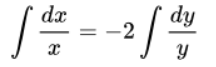
Интегральные части являются табличными, \(ln│x│ = − 2ln│y│ + ln C_1\)
Осуществляем потенцирование: \(C 1 = xy^2\)
\(y^2={-C_1 \over x}\)
Осуществляем подстановку во второе уравнение:
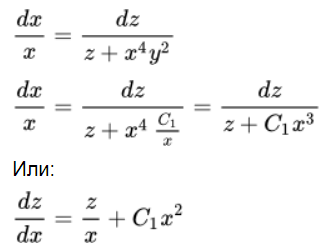
Сложно разобраться самому?
Попробуйте обратиться за помощью к преподавателям
Это линейное ДУ. Решаем с помощью интегрирующего множителя. Помножим на \(x^{-1}\) и осуществим преобразование:
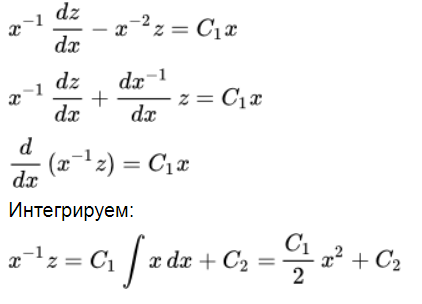
Осуществим подстановку полученного равенства \(C_1 = xy^2:\)
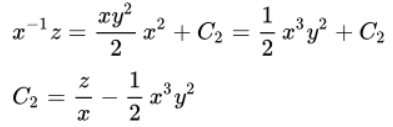
Следовательно, находим два интеграла:
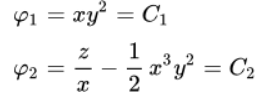
Всеобщее решение дифференциального уравнения в частных производных:
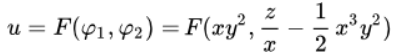
Где F является функцией от двух переменных Осуществим работу по нахождению ее вида из предельного условия
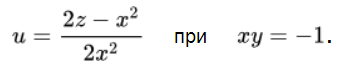
Исследуем решение дифференциального уравнения.
Предположим xy = –1:
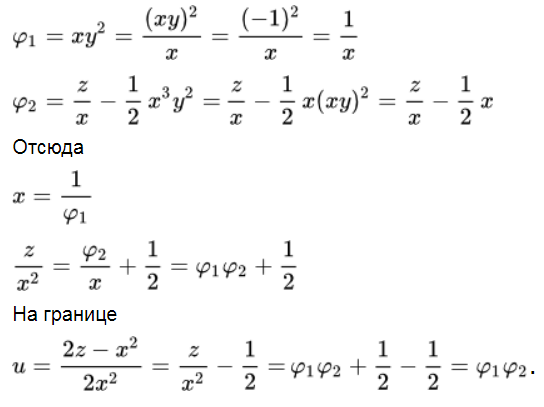
Определено, что на границе функция F обладает видом: \(F(φ_1, φ_2) = φ_1φ_2.\)
Она является аналогичной и во всей области.
Осуществив работу по подстановке данных
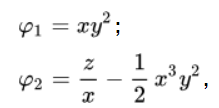
Обретаем частное решение дифференциального уравнения в частных производных с первоначальным предельным условием:
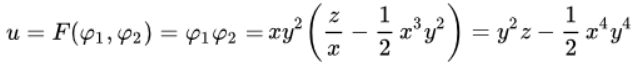
Ответ
Всеобщее решение дифференциального уравнения:
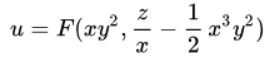
Частное решение дифференциального уравнения:
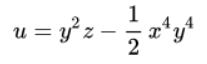
Закажите подходящий материал на нашем сервисе. Разместите задание – система его автоматически разошлет в течение 59 секунд. Выберите подходящего эксперта, и он избавит вас от хлопот с учёбой.
Гарантия низких цен
Все работы выполняются без посредников, поэтому цены вас приятно удивят.
Доработки и консультации включены в стоимость
В рамках задания они бесплатны и выполняются в оговоренные сроки.
Вернем деньги за невыполненное задание
Если эксперт не справился – гарантируем 100% возврат средств.
Тех.поддержка 7 дней в неделю
Наши менеджеры работают в выходные и праздники, чтобы оперативно отвечать на ваши вопросы.
Тысячи проверенных экспертов
Мы отбираем только надёжных исполнителей – профессионалов в своей области. Все они имеют высшее образование с оценками в дипломе «хорошо» и «отлично».
Эксперт получил деньги, а работу не выполнил?
Только не у нас!
Безопасная сделка
Деньги хранятся на вашем балансе во время работы над заданием и гарантийного срока
Гарантия возврата денег
В случае, если что-то пойдет не так, мы гарантируем возврат полной уплаченой суммы
















































Заполните форму и узнайте цену на индивидуальную работу!




