- Деформации и силы упругости
- Характеристика упругих сил
- Закон Гука
- Остаточная деформация
- Деформация сдвига
Определение 1
Силой упругости называется такая сила, которая возникает при деформации вещества и стремится вернуть его в первоначальное состояние.
На все тела вокруг нас действуют различные деформации. Они появляются из-за движения тел и изменения относительного расположения их частичек. В зависимости от степени обратимости процесса деформации, различают упругие и пластические (остаточные) деформации, или, другими словами, обратимые и необратимые.
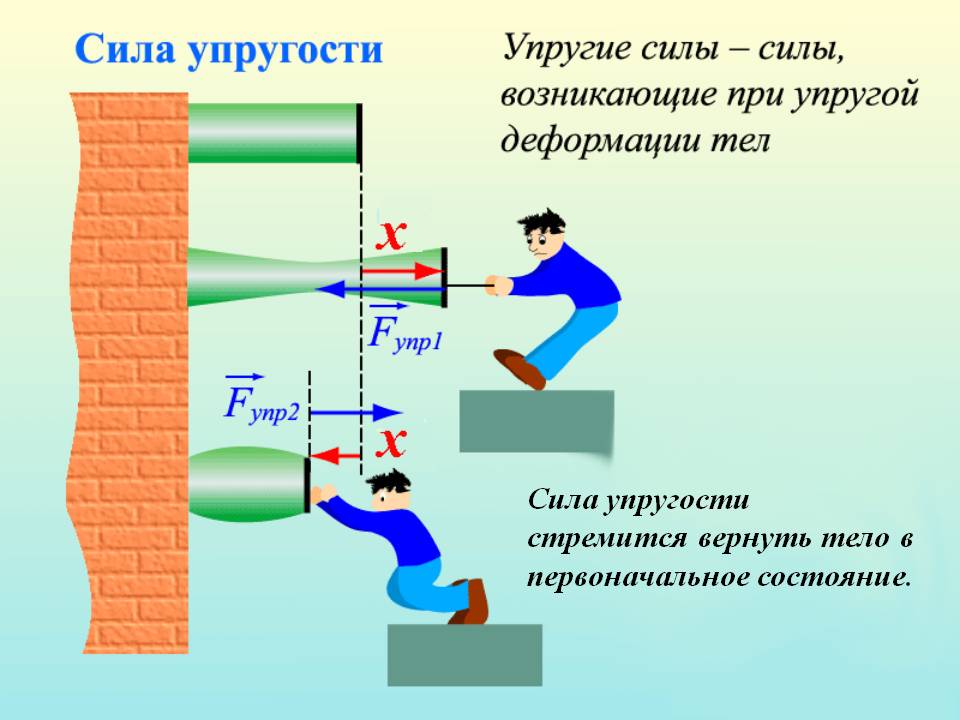
Упругой называется такая деформация, при которой тело по окончанию воздействия силы, приводящей к деформации, возвращается в первоначальное положение и сохраняет свои первоначальные параметры.
Упругая деформация возможна лишь в том случае, когда сила внешнего воздействия не больше, чем предел упругости. Другими словами, сила упругости компенсирует воздействие на тело внешней силы.
Если же воздействие внешней силы превышает предел упругости, происходит пластическая или остаточная деформация. То есть, после воздействия такой силы тело теряет свои первоначальные параметры.
Явление пластической деформации обусловлено тем, что возникающие в теле упругие силы не способны полностью противостоять воздействиям внешних сил.
Выделяют несколько видов простых деформаций:
- деформация растяжения;
- деформация изгиба;
- деформация сдвига;
- деформация кручения.
Обычно процесс деформации включает в себя совокупность нескольких таких типов одновременно, в результате этого выделяют два основных вида деформации: растяжение и сдвиг.
![banner]()
Сложно разобраться самому?
Попробуйте обратиться за помощью к преподавателям
Механическим напряжением является физическая величина, показывающая модуль силы упругости, что действует на единицу площади.
Такое механическое напряжение бывает двух видов, которые отличаются направлениям приложения упругой силы. Это нормальное σ и тангенциальное τ механическое напряжение.
Замечание 1
Количественная мера степени деформации – это относительная деформация.
К примеру, относительное изменение длины стержня описывается таким образом:
\(ε= {Δl \over l}\)
А величина относительного продольного растяжения или сжатия описывается так:
\(ε'= {Δd \over d}\)
где \(l\) – длина;
\(d\) – диаметр стержня.
Эти виды деформаций происходят одновременно, но имеют разные знаки, поскольку во время растяжения длина увеличивается, а диаметр уменьшается. Если же рассматривать процесс сжатия тела, то здесь будет всё наоборот, то есть длина будет уменьшаться, а диаметр увеличиваться. Взаимосвязь этих деформаций можно описать следующим выражением:
\(ε'=-με,\),
где \(μ\) – коэффициент Пуассона, который зависит от характеристик самого материала.
Следует отметить, что силы упругости не являются фундаментальными силами, они относятся по своей природе к электромагнитным и, соответственно, описываются приближенными формулами.
Эмпирическим путем было установлено что при небольших деформациях относительное увеличение длины и напряжение пропорциональны между собой:
\(σ=Eε,\)
где E – модуль Юнга. Значение данного коэффициента соответствует удлинению материала на одну единицу. Модуль Юнга измеряют в Ньютонах на квадратный метр, то есть в Паскалях.
В соответствии с законом Юнга удлинение стержня в процессе упругой деформации пропорционально силе действия на стержень:
\(F= {ES\over l}Δl=kΔl,\)
где k является коэффициентом упругости.
Деформацию твердых тел можно описать по закону Гука только до момента достижения предела пропорциональности. Деформация становится нелинейной после достижения предела упругости. То есть, закон Гука применим лишь при упругих деформациях.
![banner]()
Не нашли то, что искали?
Попробуйте обратиться за помощью к преподавателям
Остаточная деформация возникает при действии внешних сил за пределом упругости.
Определение 2
Величина механического напряжения, когда возникает заметная остаточная деформация, называется предел текучести \(στ\).
При дальнейшем возрастании воздействия внешней силы степень деформации растет без увеличения напряжения до величины предела прочности \(σp\), при котором тело разрушается. При графическом изображении возвращения тела к первоначальным параметрам, промежуток между точками \(στ\) и σp будет называться областью текучести или областью пластической деформации. В соответствии с размером данной области материалы делят на вязкие и хрупкие. Для хрупких материалов область текучести значительно меньше, чем для вязких.
Все вышеперечисленные явления возникают при действии внешней силы по нормали. Если внешняя сила действует по касательной, имеют место деформации сдвига.
В таком случае на каждую точку тела действует тангенциальное напряжение, которое определяется как модуль силы, действующей на единицу площади:
\(τ= {F\over S}.\)
При этом относительный сдвиг рассчитывается таким образом:
\(γ= {1\over G}τ,\)
где \(G\) является модулем сдвига.
Модуль сдвига \(G\) показывает значение тангенциального напряжения, соответствующее величине сдвига в единицу. Измеряется в Паскалях.
Мы ВКонтакте 
Трейлер о сайте 
