Спектры щелочных металлов

1. Резонансное возбуждение автоионизационных состояний атомов щелочных металлов электронным ударом
2. Уровни различных рядов
3. Решение уравнения Шредингера

Распределение интенсивности электромагнитного излучения атомов, в частности щелочных металлов, в том числе водорода, содержит в себе некоторые спектральные серии. Самые сверх интенсивные из этих серий обрели следующие наименования:

• Главная серия.
• Первые побочные или диффузные серии.
• Вторые побочные или резкие серии.
• Фундаментальные (основные) серии или серии Бергмана.

Шведский физик Йоханнес Роберт Ридберг в 1888 году представил формулы, доказанные опытным путём, позволяющие рассчитать частоту серии щелочных металлов.

Резонансное возбуждение автоионизационных состояний атомов щелочных металлов электронным ударом

Рассматривая некоторое количество спектральных серий линий, были даны им наименования на основании проведенных экспериментов:

• Главная серия линий – данные линии встречались и в спектрах поглощения и спектрах испускания, что доказывало переход атомов в основное состояние.
• Диффузная серия линий – данные линии казались расплывчатыми и не чёткими.
• Резкая серия линий – данные линии смотрелись очень чётко и ярко.
• Фундаментальная серия линий или серия Бергмана – данные линии были подобны серии линий атома водорода.

Доказано, что представленные серии линий соединены с переходами валентного или оптического электрона.

Рассмотрение итогов прошлых изучений автоионизационных явлений указывает, что из большого количества исследований более эффективными исследованиями необходимо полагать спектроскопию фотопоглощения и электромагнитную спектроскопию, соединенную с техникой пересекающихся атомных и электронных потоков. Особенно, очень хорошо изучены электронные спектры фотопоглощения атомов щелочных и щелочноземельных металлических веществ, одноатомных газов, автоионизационные спектры, а также простых молекул.

В определённых ситуациях выполнена спектроскопическая систематизация линий, совершен анализ сечений возбуждения и периода существования автоионизационных состояний (АИС). Одновременно данные итоги указали, что для надёжного толкования информации и, в частности, для определения механизма образования и распада АИС, необходимы исследования электроэнергетических соотношений сечений возбуждения, так называемой функции возбуждения (ФЗ), у границы явления, используя моноэнергетические электронные потоки.

Изучение автоионизационного состояния атомов металлов начались благодаря заведующему кафедрой квантовой электроники, Ужгородского университета, профессору И. П. Записочному. Он провел свои первые исследования ещё в начале 1970-х годов, с помощью методики электронной спектроскопии. Постоянные изучения возбуждения наружной оболочки в атомах щелочноземельных элементов показали усиление продуктивности данного процесса в приграничной сфере энергии.

Как раз те самые итоги исследований, вдобавок собранная информация по энергетическим зависимостям сечений возбуждения автоионизации, которые распадаются в оптическом канале, дали возможность допустить, что подпороговое возбуждения субвалентной р6 оболочки в атомах щелочных металлов обязан содержать отчетливый резонансный характер. Косвенным указателем была информация с сечений электронной ионизации данных металлов, где прослеживался значительное увеличение сечения на границе возбуждения р6 оболочки.

Не нашли то, что искали?

Попробуйте обратиться за помощью к преподавателям

Тип работы Выберите тип работыКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяОнлайн-репетиторЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Уровни различных рядов

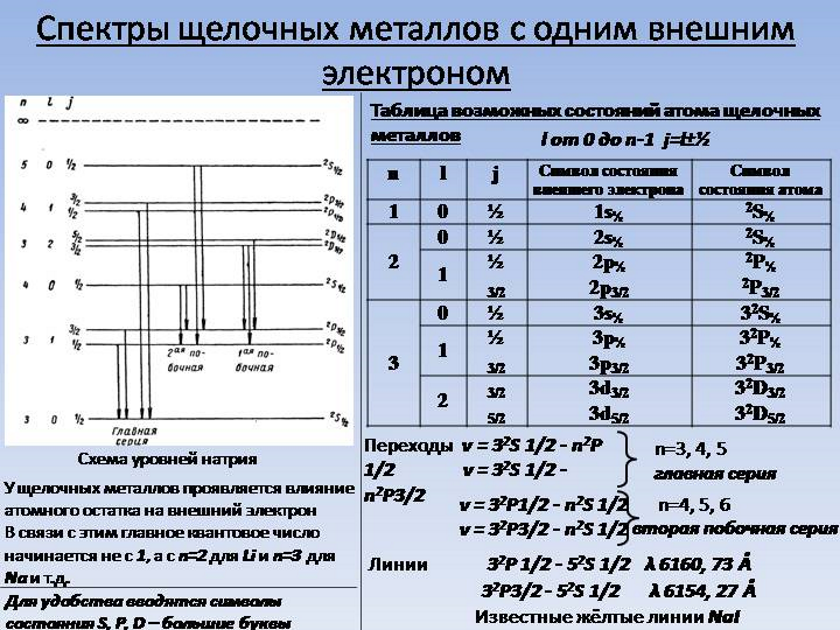
Структура уровней натрия в корне отлична от структуры уровней атомов водорода. Отличие состоит в том, что схожие уровни в отличных рядах лежат на совсем неодинаковой высоте. Однако, невзирая на данное различие, структуры обладают огромным совпадением. Это совпадение допускает, что собственно спектры щелочных металлов обладают возможностью распространяться при переходе наружного электрона с одного уровня на другой.

Разуметься, энергия состояния практически в полном объёме зависима, кроме числа \(n\), и от того, в каковом ряду окажется этот терм, другими словами от определённого номера ряда термов. На всевозможных уровнях атома водорода присутствуют всевозможных ряды термов. Они обладают характерные величины момента для всплеска электрона. Возможно допустить, что различные ряды термов щелочных металлов отличаются величинами момента всплеска действительно оптического электрона.

По тому, как уровни различных рядов в конкретной ситуации не находятся на равной высоте, нужно признать тот факт, что энергия оптического электрона в атоме щелочного металла в полном объёме зависима от значения момента всплеска электрона. При этом в более непростых атомах, имеющими некоторое количество электронов, возможно предположить, что любой электрон сможет передвигаться в усредненном поле ядра.

Таким образом это поле не является кулоновским, но обладает центральной симметрией. То есть, электроны передвигаются в атоме с чрезвычайно значительными скоростями, и поле, которое по времени усреднено, принято рассматривать, как центрально-симметричное.

Сложно разобраться самому?

Попробуйте обратиться за помощью к преподавателям

Тип задания Выберите тип заданияКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяОнлайн-репетиторЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Решение уравнения Шредингера

Результат уравнения Шрёдингера для электрона, двигающегося в центрально-симметричном не кулоновском поле, предоставляет информацию, схожую с результатом для атома водорода, однако с той разницей, что каждый энергетический уровень в полной мере зависим не исключительно от квантового числа \(n\), а ещё и от квантового числа \(l\). В частности, в этой ситуации в полной мере освобождается перерождение \(n\).

Однако различие в энергии меж пребываниями с подобными и отличными \(n\) мало, как между пребываниями с всевозможными \(n\). С пошаговым повышением энергия уровней с равными \(n\) понемногу инициализирует возрастание. Все числа устанавливают момент всплеска каждого электрона, в том числе проекцию электрона на конкретную указанную ориентацию. Действительно, момент всплеска атома в полной мере заключается из конкретных моментов электронов, они составляют структуру атома/