Возрастание и убывание функции

1. Общие понятия о поведении функций
2. Свойства монотонных функций
3. Алгоритм определения поведения функции
4. Примеры решения задач на исследование поведения функции

Общие понятия о поведении функций

Исследуя функции, заданные определенными уравнениями, особенно уделяют внимание их свойствам, а именно возрастанию или убыванию.

Монотонной функцией называется функция, меняющаяся в одном направлении.
На графиках представлены примеры монотонно возрастающей и монотонно убывающей функций.

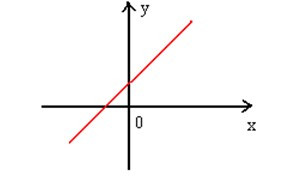
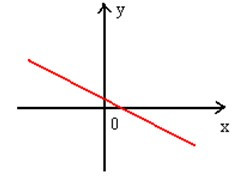
Соответственно, монотонная функция может быть возрастающая или убывающая.

Возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается, иными словами, чем больше значение аргумента, тем больше значение функции.

Математическое выражение этого определения выглядит следующим образом:

\(f(x)=↑x_1 f(x_2)\).

Убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается, иными словами, чем больше значение аргумента, тем меньшее значение функции.

Математическое выражение этого определения выглядит следующим образом:

\(f(x)=↓x_1 f(x_2)\).

Разберем примеры решения задач на изучение характера поведения функции.

Задача 1. Задана функция \(y=x^3+1\). Исследовать ее характер в интервале \([0;2]\).
Решение: Подставим поочередно крайние значения заданного отрезка и сравним полученные значения функции.
\(y_1=0^3+1=1\);
\(y_2=2^3+1=9\).

Поскольку значения функции увеличиваются, при увеличении значений аргумента, то данная функция на заданном отрезке будет возрастать.

Задача 2. Задана функция \(y={1\over x}\). Определить ее характер в интервале \([1;2]\).
Решение: Подставим поочередно крайние значения заданного отрезка и сравним полученные значения функции.
\(y_1={1\over 1}=1\);
\(y_2={1\over2}=0.5\).

Поскольку значения функции уменьшаются, при увеличении значений аргумента, то данная функция на данном отрезке будет убывать.

Не возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается или остается на том же уровне, иными словами, большему значению аргумента соответствует большее или равное значение функции.

Не нашли то, что искали?

Попробуйте обратиться за помощью к преподавателям

Тип работы Выберите тип работыКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Не убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается или остается на том же уровне, иными словами, большему значению аргумента соответствует меньшее или равное значение функции.

Постоянной называется такая функция, которая не убывает и не возрастает, то есть при увеличении или при уменьшении значения аргумента, значение функции остается на одном и том же уровне. Пример такой функции можно наблюдать на рисунке.

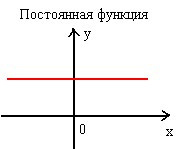
Разберем задачу на исследование характера поведения функции. При данной функции \(y=5\) исследовать ее характер в интервале \([0;2]\).

По сути эту функцию можно записать как \(y=5+0∙x\), подставляя крайние значения отрезка, получим:
\(y_1=5+0∙0=5\);
\(y_2=5+0∙2=5\).

То есть функция \(y=5\) будет постоянной.

Постоянная, не убывающая и не возрастающая функции не есть монотонные.

Свойства монотонных функций

К свойствам монотонных функций относятся такие характеристики:

• если две или больше возрастающих функций суммируются, то в результате получается тоже возрастающая функция;
• результатом произведения положительных возрастающих функций будет возрастающая функция;
• при композиции двух возрастающих функций получается также функция, которая будет возрастать;
• при положительной функции \(f(x)\), функция \(f^n (x)\) тоже будет возрастать, при условии, что \(n\) является натуральным числом;
• при сохранении возрастающей функцией \(f(x)\) своего знака, обратная ей функция будет убывать;
• при возрастающей функции \(f(x)\) и константе c справедливо, что функции \(cf(x)\) и \(f(x)+c\), при \(c>0\), будут возрастать.

Монотонность производной и заданной функций связаны между собой, и это описано в таких теоремах:

Алгоритм определения поведения функции

Алгоритм изучения функции на предмет возрастания или убывания выглядит следующим образом:

• для заданной функции находят производную;
• определяют стационарные или критические точки производной функции (f^' (x)=0 или вовсе не существует);
• рассчитывают знак производной функции в каждом из интервалов;
• определяют поведение функции в каждом из интервалов.

Примеры решения задач на исследование поведения функции

Пример 1. Дана функция следующего вида: \(y=x^3-12x\). Определить ее характер поведения в интервале \((-∞;+∞)\).
Решение:
1. Рассчитываем производную заданной функции:
\(y'=(x^3-12x)'=3x^2-12.\)

2.Производная определяется на всем промежутке:
\(y'=0 ⇒ 3x^2-12=0 ⇒3x^2=12 ⇒x^2=4 ⇒ x=±2,\)
\(x=±2\) являются стационарными точками.

3. Изучаем знак производной функции при помощи числовой прямой:

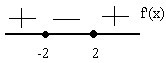
\(y' (0)=3∙0^2-12=-12\);
\(y' (-3)=3∙(-3)^2-12=15\);
\(y' (3)=3∙3^2-12=15\).

То есть производная положительна в интервалах \( (-∞;-2]\) и \([2;+∞)\), и отрицательна в интервале\( [-2;2]\).
4. Определяем характер поведения функции:

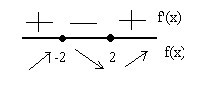
Согласно выше рассмотренных теорем, заданная функция будет убывать в интервале \([-2;2]\), и возрастать в интервалах \(- (-∞;-2]\) и \([2;+∞)\).

Сложно разобраться самому?

Попробуйте обратиться за помощью к преподавателям

Тип задания Выберите тип заданияКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Пример 2. Дана функция следующего вида: \(y={x\over(x-2)}\). Определить ее характер поведения в интервале(-∞;+∞).
Решение:
1. Находим производную функции:
\(y'=({x\over x-2})'={1∙(x-2)-x∙1\over(x-2)^2} ={x-2-x\over x-2^2} =-{2\over(x-2)^2}\) .

2. При \(x=2\) производная функция будет неопределенной. Стационарные точки не обнаружены.

3.Изучаем знак производной при помощи числовой прямой:

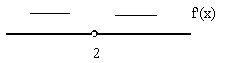
\(y' (0)=\)\(-{2\over(0-2)^2} =\)\(-{2\over(-2)^2} =\)\(-{2\over(0-2)^2}\) =\(-{2\over4}=-0,5\);
\(y' (4)=-{2\over(4-2)^2} =\)\(-{2\over(2)^2} =-{2\over4}=-0,5\).
То есть производная функция отрицательна на определяемых участках.

4.Определяем характер поведения функции.

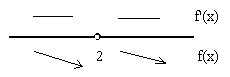
Согласно теореме 2, при отрицательной производной, заданная функция убывает. То есть на всем определяемом промежутке заданная функция будет убывающей.