Законы астрономии

1. Законы Кеплера
   1. Первый закон Кеплера
   2. Второй закон Кеплера
   3. Третий закон Кеплера
2. Закон всемирного тяготения
3. Закон Хаббла

Основными законами, используемыми в астрономии, являются следующие законы:

• Законы Кеплера;
• Закон Ньютон или закон всемирного тяготения;
• Закон Хаббла (о разбегании галактик).

Законы Кеплера

В 1619 году немецкий астроном, механик и математик Иоганн Кеплер (1571-1630 г) опубликовал свою книгу «Гармония мира», в которой вывел ряд астрономических законов, связанных с движением планет.

Кеплер утверждал, что планетарные орбиты имеют эллипсовидную форму, одним из фокусов которой является Солнце. Площадь векторов от Солнца до планеты равнозначные за равные интервалы времени. Квадраты времени обращения планет вокруг Солнца относятся между собой с такой же пропорцией, как их средние расстояния до Солнца, возведенные в куб.

Первый закон Кеплера

Для планет характерна траектория в виде замкнутой кривой в форме эллипса. Каждая орбита имеет два фокуса – точки, расположенные внутри орбиты на постоянных расстояниях. Кеплер выяснил, что все орбитальные планетарные траектории имеют одну плоскость. Наиболее вытянутые орбиты  у Марса и Плутона, у остальных планет форма орбиты близка к окружности. Именно поэтому Первый закон Кеплера часто называют законом эллипсов.

Сложно разобраться самому?

Попробуйте обратиться за помощью к преподавателям

Тип задания Выберите тип заданияКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяОнлайн-репетиторЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Второй закон Кеплера

Планетарные скорости достигают наибольшего значения в случае, когда планета находится на минимальном расстоянии от Солнца. Соответственно, наименьшие значения достигаются, когда расстояние от Солнца максимальное. Согласно Второму закону Кеплера, все планеты обращаются в плоскости, проходящей через солнечный центр. Радиус-вектор, который соединяет Солнце с планетой, за равные временные промежутки очерчивает равные площади.

Третий закон Кеплера

Квадраты периодов полного обращения планет соотносятся в той же степени, что и кубы наибольших полуосей орбит этих планет.

Этот закон отображает взаимосвязь между периодом орбитального обращения и расстоянием от планеты до Солнца.

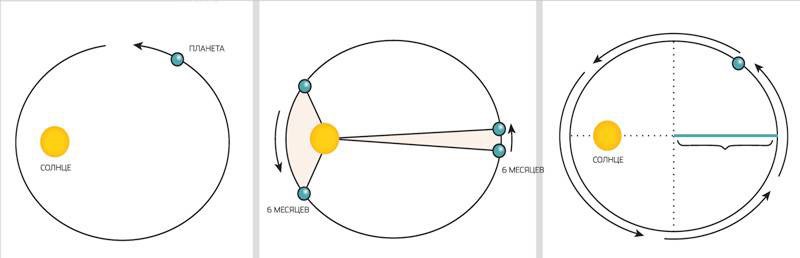
Рисунок 1. Законы Кеплера (а - первый, б - второй, в – третий).

Закон всемирного тяготения

Английский физик и математик Исаак Ньютон (1643-1727 гг) сформулировал закон всемирного тяготения, гласящий, что любые тела влияют друг на друга посредством взаимного притяжения. Участвующие в этом процессе силы называются гравитационными или силами всемирного тяготения и проявляют себя на любых объектах Вселенной.

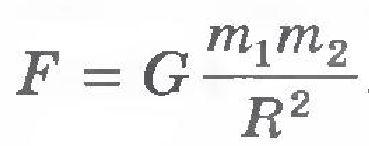
Рисунок 2. Закон всемирного тяготения 

Именно Ньютон предложил формулу закона всемирного тяготения, где:

• \(G\) - гравитационная постоянная, 
• \(m_1\) и \(m_2\) - массы взаимодействующих тел, 
• \(r\) - расстояние между ними, 
• \(F\) - сила притяжения

Для закона всемирного тяготения принята формулировка, что любые материальные тела взаимно притягивают друг друга с силой, которая прямо пропорциональна произведению их масс и обратно пропорционально квадрату расстояния между ними. Действие силы происходит вдоль линии, соединяющей эти тела.

Не нашли то, что искали?

Попробуйте обратиться за помощью к преподавателям

Тип работы Выберите тип работыКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяОнлайн-репетиторЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Гравитационная постоянная имеет физический смысл, который вытекает из закона всемирного тяготения. В том случае, если массы равны 1 кг, расстояние между ними равно 1 м, то гравитационная постоянная \(G\) равняется силе притяжения \(F\), то есть наблюдается равенство силы притяжения и гравитационной постоянной.

Гравитационная постоянная \(G\) равняется ,\(67•10−11 Н м к г Н•м^2/кг^2.\)

Действие гравитационных сил происходит между любыми материальными объектами, но при маленьких массах оно не ощущается, а ощущается только в том случае, если масса одного тела несоизмеримо больше массы другого. Пример – сила притяжение на Земле или любой другой планете, так именуемая силой тяжести. Именно сила тяжести придется тела ускорение свободного падения.

Сила тяжести всегда направлена к центру Земли или планеты. Когда тело движется с ускорением, его вес определяется как : \(P=M•(g+a)\), где \(a\) - ускорение поднимающегося или падающего тела. Поэтому при движении тела в космосе или при свободном падении возникает невесомость, так как масса тела имеет нулевое значение.

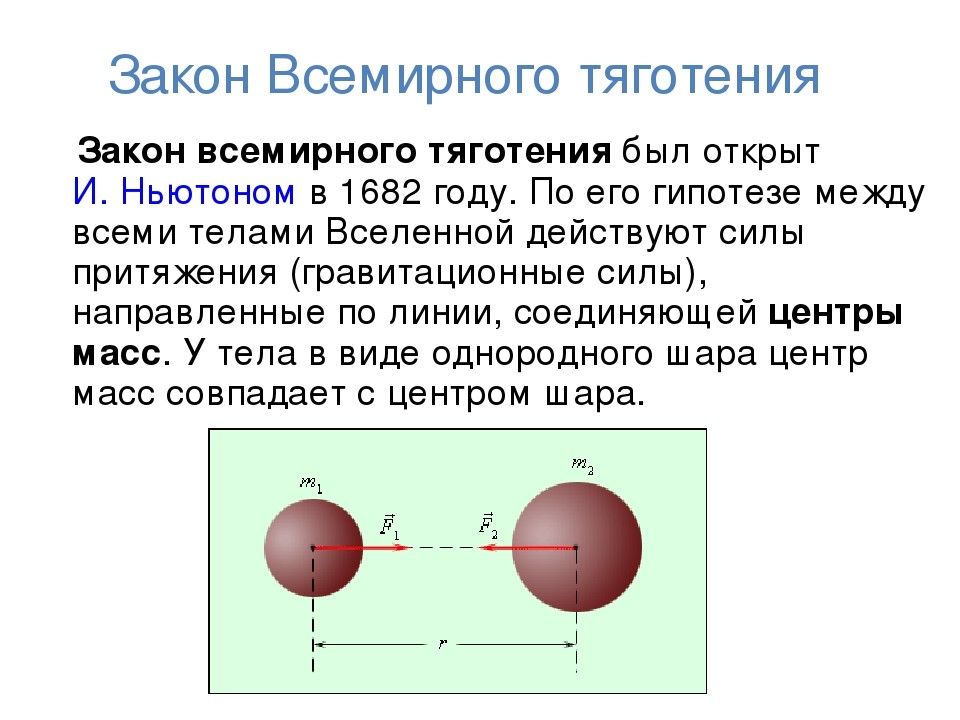
Рисунок 3. Закон всемирного тяготения 

Закон Хаббла

Американский астроном Эдвин Хаббл (1889-1953 г) является открывателем закона, который доказывает, что Вселенная постоянно расширяется. Также он установил, что расширение Вселенной характеризуется однородностью и изотропией, проще говоря Вселенная расширяется во всех направлениях с одинаковой скорость.

Закон Хаббла, помимо теории о расширении Вселенной, также доказывает и теории об ее образовании, так называемую теорию Большого взрыва. Наиболее распространенная формулировка закона Хаббла выглядит следующим образом:

\(V=h_0•R\), где:

• \(V\) - галактическая скорость, 
• \(h_0\) - коэффициент пропорциональности, связывающий дистанцию между Землёй и космическим объектом со скоростью его отдаления (так называемая «Постоянная Хаббла»),
• \(R\) - расстояние до галактической структуры. 

Существует и иная запись закона Хаббла: \(C•Z=h_0•R\), где: 

• \(C\) - скорость света, 
• \(Z\)  - красное спектральное смещение - сдвиг линий спектра, создаваемых химическими элементами при их удалении, в красную длинноволновую сторону.

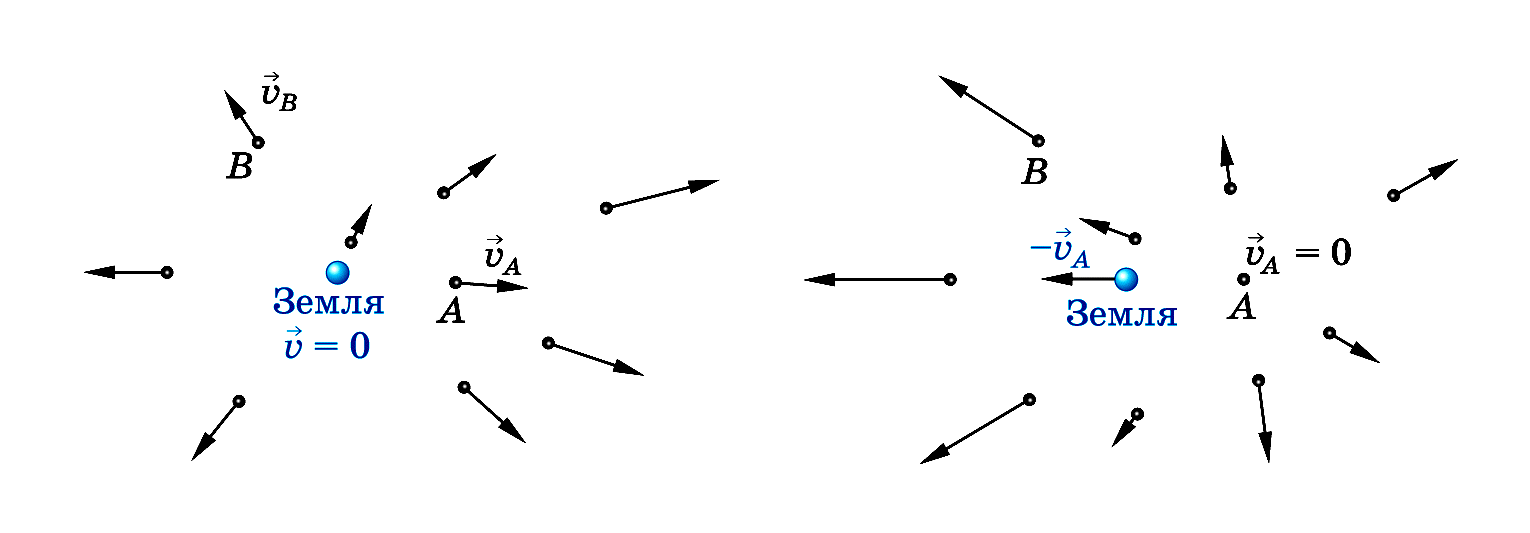
В астрономии закон Хаббла занимает очень важное место, так как широко используется для подтверждения различных научных гипотез, а также в наблюдениях за космосом и космическими телами. Но основным значением закона Хаббла является постулат о постоянном расширении Вселенной, а также именно он доказывает гипотезу Большого Взрыва.