Биномиальное распределение

Случайной или измеримой величиной называют такую действительную функцию \(ξ=φ(ω)\), которая определена в измеримом пространстве \( {Ω,F}\), при

\(∀B⊂B(R):{ω: φ(ω)⊂B}⊂F\)

или прообраз \(f^(-1^) (B)={ω: φ(ω)⊂B}\) есть измеримым множеством в \( Ω\).

Распределением вероятностей случайной величины \(ξ\) в измеримом пространстве\( {R,B(R)}\) есть вероятностная мера \(P_ξ\) на \({R,B(R)}\) с вероятностью \(P_ξ=P{ ω: φ(ω)⊂B},B⊂ B(R)\).

Функция распределения случайной величины \(ξ=φ(ω)\) выглядит следующим образом:

\(F_ξ (x)=P(ξ.

Дискретные случайные величины

Дискретной случайной величиной есть такая величина, что для каждого элементарного события ω находит соответствующее одно из счетного или конечного набора

\(x_1,x_2,x_3,…,x_n,n∈N={1,2,3,…}.\)

Ряды распределения предназначены для выражения дискретной случайной величины в полной мере.

Не нашли то, что искали?

Попробуйте обратиться за помощью к преподавателям

Тип работы Выберите тип работыКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

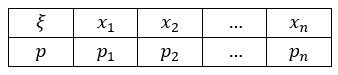
В том случае, если дискретная случайная величина \(ξ\) имеет значения \(x_1, то ряд ее распределения представляется в виде таблицы, состоящей из двух строчек. В верхней строчке будут находиться все вероятные значения \(x_i\), которые может принять величина, а в нижней – вероятности этих значений \(p_i=P(ξ=x_i)\), при этом \(∑_ip_i =1\).
 

Непрерывная случайная величина – это функция \(ξ=φ(ω)\), множество значений которой принимает некий интервал чисел \((a,b), a,b∈R\).

Плотность распределения вероятностей непрерывной случайной величины \(ξ\) – это функция \(ρ_ξ (x)\), удовлетворяющая следующим условиям:

1. \(∀x∈Rρ_ξ (x)≥0\);
2. \(∫_{(-∞)}^∞ρ_ξ (x)dx=1\). 

Соответственно:

\(F_ξ (x)=∫_{(-∞)}^xρ_ξ (t)dt\).

Если значения случайной величины есть числом наступлений некого события \(A\) по схеме Бернулли из \(n\) испытаний, то считается, что она распределяется по биномиальному закону. Записывается в ряд распределения, который выглядит так:

Общее количество \(ξ\) появлений события \(A\) в \(n\) испытаниях состоит из количества появлений этого события в отдельных не зависящих друг от друга испытаниях \(ξ_i\), где i=\(1,2,…,n, ξ_i\) –  случайная величина, что равна количеству наступлений события \(A\) в \(i\)-том испытании. В данном случае распределение каждой случайной величины будет иметь такой вид:

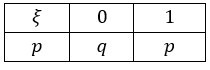
Из этого следует, что математическое ожидание:

\(M(ξ_i )=∑_{(i=1)}^2x_i∙p_i=0∙q+1∙p=p\).

Используя свойства математического ожидания, получаем дисперсию:

\(D(ξ_i )=∑_{(i=1)}^2 x_i^2∙p_i-M^2 (ξ_i )=0^2∙q+1^2∙p-p^2=p-p^2=p∙(1-p)=p∙q\).

Пример на тему

Задача. Есть партия однотипных деталей, 90% деталей в которой – стандартные. Берут случайных 5 деталей. Необходимо определить закон распределения дискретной случайной величины \(ξ\) – количества нестандартных деталей среди отобранных пяти. Записать функцию \(F_ξ (x)\).

Сложно разобраться самому?

Попробуйте обратиться за помощью к преподавателям

Тип задания Выберите тип заданияКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Решение: Случайная величина \(ξ\), представленная целыми числами, по биномиальному закону распределения принимает следующие значения \(ξ=0,1,2,3,4,5\).

В соответствии с условием задачи, определим вероятность попадания нестандартной детали:
\(p=1-0.9=0.1\),

при этом вероятность появления стандартной детали \(q=1\), и \(n=5\).

В таком случае \(P_5 (k)=C_5^k∙p^k∙q^(n-k)\), где \(k=0,1,2,3,4,5\).

Закон распределения случайной величины \(ξ\) принимает следующий табличный вид:

Для проверки правильности решения, подставим значения в условие нормирования:
\(∑_(i=0)^5p_i=0,59049+0,32805+0,0729+0,0081+0,00045+0,00001\).

Так как условие нормирование подтверждается, то закон распределения построен верно.

Запишем функцию распределения вероятностей выбора нестандартной детали из 5 случайных, она выглядит так:

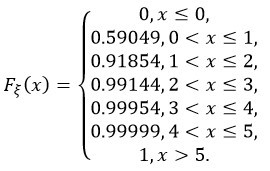
Математическое ожидание данной случайной величины \(x\), которая распределена по биномиальному закону, будет равно:

\(M(x)=5∙0.1=0.5\),

а дисперсия равна:

\(D(x)=5∙0.1∙0.9=0.45\).