Теорема Пифагора

1. Общие понятия
2. Теорема Пифагора
3. Теорема, обратная теореме Пифагора

Общие понятия

Прежде, чем перейти к формулировке самой теоремы Пифагора, рассмотрим общие понятия на эту тему.

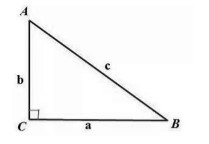
Разберем прямоугольный треугольник \(ABC\) с катетами размером \(BC=a\), \(AC=b\) и гипотенузой \(AB=с\).

Рассмотрим также теоремы о площади квадрата и треугольника.

1. Площадь квадрата равняется квадрату размера ее стороны и рассчитывается по формуле:

\(S=a^2.\)

2. Площадь треугольника равняется половине произведения длины его стороны и высоты, опущенной к ней, и определяется по формуле:

\(S={1\over 2 ah}\)

Теорема Пифагора

Разберем формулировку теоремы Пифагора и ее доказательство.

Теорема: Сумма квадратов катетов прямоугольного треугольника равняется квадрату его гипотенузы. Формула теоремы Пифагора выглядит следующим образом:

\(a^2+b^2=c^2\)

Доказательство: Допустим у нас имеется прямоугольный треугольник со сторонами \(a,b,c,\) как на рисунке выше. Достроим к нему квадрат со стороной \(a+b\).

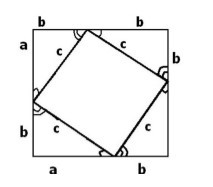
Площадь построенного квадрата будет равняться сумме площадей четырех прямоугольных треугольников и квадрата со стороной \(c\). Используя теоремы о площадях фигур математически рассчитаем:

\(S=(a+b)^2=a^2+2ab+b^2,\)

Площадь внутреннего квадрата будет равна:

\(S''=c^2\).

Площадь прямоугольного треугольника будет вычисляться по формуле:

\(S'={1\over2} ab\).

В итоге выражение для площади большого квадрата можно записать следующим образом:

\(S=S''+4S'\);
\(a^2+2ab+b^2=c^2+2 ab\);
\(a^2+b^2=c^2\).

Что и требовалось доказать.

Теорема, обратная теореме Пифагора

Теорема: Если для треугольника со сторонами \(a,b,c\) выполняется равенство \(a^2+b^2=c^2\), то он является прямоугольным с гипотенузой \(c\).

Доказательство: Допустим у нас имеется прямоугольный треугольник как на первом рисунке. Изобразим рядом прямоугольный треугольник \(A' B' C'\), прямой угол у которого \(C, A' C'=AC, B' C'=BC\).

Согласно теореме Пифагора, получаем:

\((A' B')^2=(A' C')^2+(B' C')^2\);
\((A' B')^2=a^2+b^2\).

А это значит, что \((A' B')^2=AB^2\), следовательно  \(A' B'= AB\).

В соответствии с третьим признаком равенства треугольников \(ΔABC=ΔA' B' C'\), значит угол \(C\) – прямой, а \(ΔABC\) – прямоугольный. Что и требовалось доказать.

Сложно разобраться самому?

Попробуйте обратиться за помощью к преподавателям

Тип задания Выберите тип заданияКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Решение задач на данную тему

Задача 1. Задан равнобедренный прямоугольный треугольник с боковой стороной, равной 8 см. Найти его основание.

Решение: Обозначаем основание треугольника буквой \(x\).

Так как у нас треугольник прямоугольный, мы можем использовать теорему Пифагора:

\(x^2=8^2+8^2=64+64=128; x=\sqrt{128}=8\sqrt2\).

Ответ: основание треугольника равно \(8\sqrt2\).

Задача 2. Из заданных вариантов треугольников найти прямоугольные. Стороны треугольников приведены:
а) 5,12,13;
б) 6,5,4;
в) 3,4,5.

Решение: Для определения принадлежности треугольников используем теорему, обратную теореме Пифагора. Подставляем по очереди заданные значения сторон в выражение \(a^2+b^2=c^2\) и определяем справедливость равенства.

а) \(13^2=12^2+5^2; 169=169\) – равенство выполняется, а это означает, что первый треугольник является прямоугольным.

б) \(6^2=4^2+5^2; 36=41\) – равенство не выполняется, это означает, что второй треугольник не прямоугольный.

в) \(5^2=4^2+3^2; 25=25\) – равенство выполняется, а это означает, что третий треугольник является прямоугольным.

Не нашли то, что искали?

Попробуйте обратиться за помощью к преподавателям

Тип работы Выберите тип работыКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Стоит обратить внимание, что прямоугольные треугольники, у которых стороны равняются целым числам, именуют пифагоровые (как в варианте «а»), а со сторонами, у которых значения представлены поочередными натуральными числами – египетские (как в варианте «в»).