Расстояние между двумя параллельными прямыми в пространстве

1. Базовые понятия и теоремы
2. Доказательство теоремы про расстояние между параллельными прямыми
3. Примеры определения расстояния между параллельными прямыми

Для лучшего понимания темы рассмотрим основные понятия, термины и теоремы, связанные с параллельными прямыми.

Базовые понятия и теоремы

Расстоянием есть такая величина, которая характеризует отдаленность объектов друг от друга. Это определение применимо для плоскости и для пространства. Зачастую расстояние измеряют при помощи различных измерительных приборов, таких как линейка, штангенциркуль и прочих. При передвижении на машине расстояние вычисляют с помощью спидометра. На больших расстояниях применяют различные вычисления для определения величины расстояния.

Две прямые являются параллельными в трехмерном пространстве только в том случае, если они находятся в одной плоскости и не пересекаются. Это значит, что параллельность прямых определяется двумя критериями:

• они должны находиться в одной плоскости;
• они не имеют ни одной совместной точки.

Но не нужно путать параллельные прямые со скрещивающимися, они тоже никогда не пересекаются и не имеют общих точек, но их невозможно расположить в одной плоскости.

Сложно разобраться самому?

Попробуйте обратиться за помощью к преподавателям

Тип задания Выберите тип заданияКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяОнлайн-репетиторЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Если рассмотреть примеры из жизни, то параллельные прямые мы можем наблюдать как противоположные края у прямоугольного или квадратного стола, железнодорожные рельсы и шпалы, провода линий электропередач, линии в тетради в полоску и прочие. Таких примеров из реального мира можно привести очень много.

Расстоянием между параллельными прямыми является перпендикулярный отрезок между этими прямыми. Он может быть проведен в любом месте между ними и везде будет одинаковым. Рассмотрим доказательство этой теоремы.

Доказательство теоремы про расстояние между параллельными прямыми

Изобразим две параллельные прямые \(l\) и \(k\). Возьмем две случайные точки на прямой \(l\), назовем их например \(X\) и \(Y\), опустим с них перпендикуляры на прямую \(k\). Совершенно не имеет значения какие именно мы возьмем точки, главное, чтобы они не совпадали, то есть между ними должно быть некоторое расстояние.

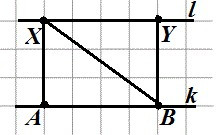
Назовем точки пересечения прямой k с перпендикулярами \(A\) и \(B\).

Проведем отрезок \(XB\), который является гипотенузой прямоугольника \(XYBA\) получившиеся углы \(XBA\) и \(BXY\), находящиеся накрест друг от друга, будут равны. гипотенуза \(XB\) пересекает данные прямые.

Рассмотрим треугольники \(XBA\) и \(BXY\), определим их общие элементы:

• они имеют общую сторону \(XB\);
• стороны треугольников \(XY\) и \(AB\) имеют одинаковую длину;
• величина углов \(XBA\) и \(BXY\) одинаковая, и данные углы образованы равными между собой сторонами.

Все вышесказанное указывает на то, что треугольники \(XBA\) и \(BXY\) равны, согласно первому признаку равенства треугольников, соответственно, перпендикуляры \(AX\) и \(BY\) тоже равны.

Это соотношение будет справедливым при любых случайных точках \(X\) и \(Y\), это значит, что величины перпендикуляров между двумя параллельными прямыми, опущенных в любом месте, будут иметь одинаковое значение.

Доказательство этой теоремы справедливо как для планиметрии, так и для 3D-пространства, так как две параллельные прямые в любом случае образуют плоскость.

Примеры определения расстояния между параллельными прямыми

Рассмотрим задачу на определение расстояния меду параллельными прямыми в пространстве.

Задача 1. Даны две параллельные прямы \(l\) и \(k\). Определить расстояние между ними.

Решение: Согласно вышеизложенной теоремы, расстоянием между двумя параллельными прямыми является величина перпендикуляра между ними. Выберем произвольную точку на одной из прямых и опустим с нее перпендикуляр на другую прямую. длина этого перпендикулярного отрезка и будет решением этой задачи.

Практически не всегда удобно графически решать данные задачи, так как не всегда есть возможность выполнить рисунок в масштабе 1:1, поэтому их решают аналитическим путем, используя специальные уравнения.

Не нашли то, что искали?

Попробуйте обратиться за помощью к преподавателям

Тип работы Выберите тип работыКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяОнлайн-репетиторЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Выше мы рассматривали, что не имеет значения с какой именно точки опущен перпендикуляр, ведь все они равны между собой, поэтому решение задачи сводится, по сути, к определению расстояния между точкой, расположенной на одной из прямых, и второй прямой.

Значит, уравнение определения расстояния между прямыми \(l\) и \(k\) имеет следующий вид:

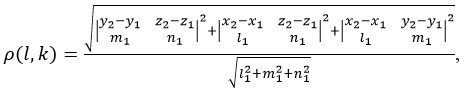
где \(x_1, y_1, z_1\) – координаты вектора нормали прямой \(l\);
       \(x_2, y_2, z_2\) – координаты вектора нормали прямой \(k\);
      \( l, m_1, n_1\) – координаты направляющего вектора прямой \(l\).

Рассмотрим пример решения задачи с использованием данного уравнения.

Задача 2. При заданных уравнениях двух параллельных прямых, что не совпадают, определить расстояние между ними.

Уравнения прямой \(l\): \( {x+1\over1}={y-2\over3}={z+4\over5x} \), прямой \(k\): \({x-3\over1}={y+1\over3}={z-2\over5} \).

Решение: Определим из уравнения координаты вектора нормали к прямой \(l\) {-1;2;-4}, к прямой \(k\) {3;-1;2}. Координатами направляющего вектора для прямой \(l\) будут {1;3;5}. Значит уравнение примет вид:

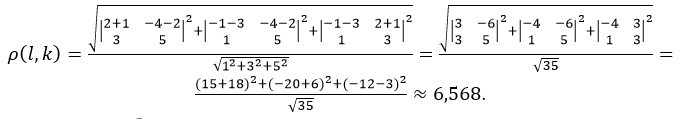
Для кого-то этот способ покажется сложным, а для кого-то простым. Всего лишь нужно уметь решать выражения матричного вида.

Рассмотрим еще один способ решения подобной задачи. Это способ алгоритма с векторным произведением.

Задача 3. Определить расстояние между параллельными прямыми способом векторного произведения. Уравнения прямых заданы в задаче 2.

Решение: Применим формулу векторного произведения:

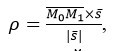
где \(M_0 M_1\) – вектор, который соединяет две случайные точки на параллельных прямых.

Вектора нормали для прямой \(l\) {-1;2;-4} и для прямой \(k\) {3;-1;2}. Координатами направляющего вектора для обоих прямых будут s={1;3;5}, так как вектор нормали у них совпадает.

Определим разность между направляющими векторами, она и будет являться координатами вектора

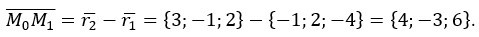
Рассчитаем векторное произведение:

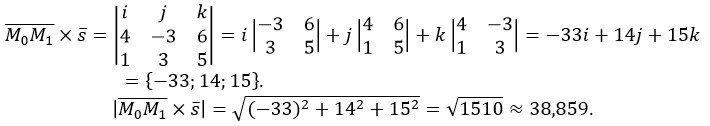
Теперь рассчитаем длину направляющего вектора:
\(|s ̅ |= \pm \sqrt{1^2+3^2+5^2 } =5,916\)

В итого расстояние между заданными прямыми будет равняться:
\(ρ= {38,859\over5,916}=6,568\)

То есть мы получили по сути тот же ответ, значит оба решения правильные и могут применяться для решения задач на определение расстояния между двумя параллельными прямыми.