






1. Виды световых лучей
2. Понятие о двойном лучепреломлении
3. Частые примеры двойного преломления лучей
4. Закон Малюса
5. Поляризация в процессе двойного лучепреломления

Различают обыкновенный и необыкновенный лучи света.
Обыкновенный луч имеет вектор \(E_0 ⃗\) который направлен нормально к главной плоскости, на его скорость не влияет направление вектора, и она равняется скорости луча с направлением, коллинеарным оптической оси. Все величины, которые имеют отношение к обыкновенному лучу обозначаются индексом 0.
Необыкновенный луч имеет вектор \(E_0 ⃗\), находящийся на главной плоскости, на скорость его распространения влияет направление, при чем если луч меняет направление, то меняется главная ось в разрезе эллипсоида. Все величины, которые имеют отношение к обыкновенному лучу обозначаются индексом е.
Отношение скоростей отрицательных кристаллов: \(v_0 v_е\).
Двойное лучепреломление представляет явление раздвоения луча, проходящего сквозь кристалл. Это происходит благодаря тому, что лучи внутри кристалла могут распространяться с разной скоростью, что приводит к возникновению в процессе преломления нескольких лучей.
Этот эффект открыл в 1669 году ученый Э. Бартолинус, а исследовал и объяснил Х. Гюйгенс.
При перпендикулярности оптической оси относительно поверхности кристалла луч будет падать вдоль оптической оси, в этом случае характер его распространение будет таким же, как в изотропной среде, то есть двойного лучепреломления не будет. Если луч будет направляться под углом к поверхности кристалла, то двойное лучепреломление будет иметь место. При этом оно будет разным для разных типов кристаллов. Для отрицательного кристалла картина будет следующей: обыкновенный луч будет преломляться больше, чем необыкновенный. В случае с положительным кристаллом картина будет противоположная: необыкновенный луч будет преломляться сильнее, чем обыкновенный.
Сложно разобраться самому?
Попробуйте обратиться за помощью к преподавателям
Если рассмотреть ситуацию, когда оптическая ось расположена параллельно поверхности кристалла, и луч направляется перпендикулярно поверхности кристалла, то в кристалле появятся два луча – обыкновенный и необыкновенный, но в пространстве они не будут разделяться. При выходе из кристалла они будут иметь разницу в фазах и создавать эллиптически поляризованную волну из-за суперпозиции. При подобном попадании на поверхность кристалла луча естественного света, выходящие из кристалла волны будут эллиптически поляризованными з разнообразными ориентированиями эллипсов.
Если на такой кристалл свет будет направлен под углом, то на двойное лучепреломление будет влиять угол между главной плоскостью и плоскостью направления луча.
Если допустить, что плоскость направления луча света расположена перпендикулярно оптической оси, и в ней расположены оба луча, то на преломление обыкновенного и необыкновенного лучей не будут влиять направления.
Если же плоскость распространения лучей расположена к оптической оси под углом отличным от 900, то ситуация с двойным лучепреломлением будет намного сложнее. Обыкновенный луч в данной ситуации будет расположен в плоскости падения, а необыкновенный окажется вне ее. Чтобы увидеть детальную картину, необходимо построить пространственную модель на базе построений Гюйгенса.
Закон Малюса позволяет определить интенсивность колебаний обыкновенного \(I_0\) и необыкновенного лучей \(I_e\), при перпендикулярном направлении луча на пластину, вырезанную из кристалла параллельно оптической оси.
Закон Малюса записывается так:
\(I_e=I_0*cos^2 α,\)
где \(α\) – угол между оптической осью и линией колебания вектора.
Вектор волны, которая падает на поверхность, раскладывается на параллельные и перпендикулярные относительно оптической оси составляющие. Эти составляющие являются векторами обыкновенной и необыкновенной световых волн.
Плоско поляризованные обыкновенный и необыкновенный лучи располагаются в плоскостях, перпендикулярных между собой. То есть эффект двойного лучепреломления применяют при создании поляризации света. С этой целью лучи света разделяют в пространстве, а один из них подвергают уничтожению посредством поглощения.
Если выходящий из кристалла один луч плоско поляризованный, а второй очень слабый, то этот кристалл является поляроидом. Примером хорошего поляроида есть турмалин. С толщиной всего в 1 мм, турмалиновая пластина практически полностью уничтожает обыкновенный луч. Электрический вектор необыкновенного луча в это время производит колебания вдоль оптической оси.
Не нашли то, что искали?
Попробуйте обратиться за помощью к преподавателям
Поляризатором является такой поляроид, который применяют при создании поляризованного света. Если его применяют для анализирования поляризованного света, то он именуется анализатором.
Рассмотрим пример решения задачи из области поляризованного света.
Ситуация с прохождением светового луча сквозь двоякопреломляющую призму. При этом преломление обыкновенного луча равняется \(n_0\)=1.658, необыкновенного \(n_е\)=1.486. Угол призмы равняется \(α\)=15. Найти угол необыкновенного луча, выходящего из призмы.
Решение: Кристаллы, поляризующие свет, в совокупности имеют название поляризационная или двоякопреломляющая призма. Поляризационной она является тогда, когда при выходе из нее остается один луч, а двоякопреломляющей – если два луча.
Если обыкновенный луч направляется через границу сред с перпендикулярными друг к другу оптическими осями, то во второй среде он становится необыкновенным. Та же картина наблюдается при прохождении необыкновенного луча.
Обозначим максимальный угол преломления необыкновенного луча \(θpre\), угол преломления луча при выходе из кристалла \(θpre\). Тогда закон преломления запишется в таком виде:
\( {sin(α-θpre) \over sin( θpre')} = {1 \over n_e}\) ,
где углом падения необыкновенного луча на границу выхода из вещества является \(α-θpre\) .
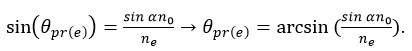
Подставив данные получим:
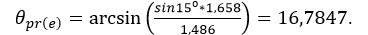 .
.
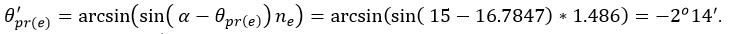
Результат решения: 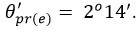 .
.
Закажите подходящий материал на нашем сервисе. Разместите задание – система его автоматически разошлет в течение 59 секунд. Выберите подходящего эксперта, и он избавит вас от хлопот с учёбой.
Гарантия низких цен
Все работы выполняются без посредников, поэтому цены вас приятно удивят.
Доработки и консультации включены в стоимость
В рамках задания они бесплатны и выполняются в оговоренные сроки.
Вернем деньги за невыполненное задание
Если эксперт не справился – гарантируем 100% возврат средств.
Тех.поддержка 7 дней в неделю
Наши менеджеры работают в выходные и праздники, чтобы оперативно отвечать на ваши вопросы.
Тысячи проверенных экспертов
Мы отбираем только надёжных исполнителей – профессионалов в своей области. Все они имеют высшее образование с оценками в дипломе «хорошо» и «отлично».
Эксперт получил деньги, а работу не выполнил?
Только не у нас!
Безопасная сделка
Деньги хранятся на вашем балансе во время работы над заданием и гарантийного срока
Гарантия возврата денег
В случае, если что-то пойдет не так, мы гарантируем возврат полной уплаченой суммы
















































Заполните форму и узнайте цену на индивидуальную работу!




