Импульсное магнитное поле

1. Квазистационарная система
2. Принципиальная схема создания импульсного магнитного поля
3. Применение импульсных магнитных полей

Импульсное магнитное поле имеет широкое распространение при физических исследованиях, а также в области прогрессивных технологий. Оно имеет применение в некоторых испытаниях, например, исследованиях управляемого термоядерного синтеза, технике сильноточных пучков заряженных частиц. При этом хватает присутствия магнитного поля на протяжение 0,1 с.

Обычно создать импульсное магнитное поле намного проще, чем постоянное с той же магнитной индукцией. А для генерирования магнитного поля с величиной индукции, превышающей 10 Тл, импульсный метод является единственным осуществимым.

Импульсное магнитное поле может быть сильным и сверхсильным.
Для того, чтобы сгенерировать импульсное магнитное поле, нужно наличие генератора импульсного тока большой силы. К подобным источникам относятся:

•  батарея электроконденсаторов;
•  аккумулятор;
•  специальный генератор переменного тока;
•  магнитный индуктор.

Квазистационарная система

При пропускании короткого импульса тока сквозь соленоид магнитное поле в окружающем пространстве меняется как по величине, так и конфигуративно.

Конфигурация магнитного поля изменяется из-за распределения тока в обмотке, это явление получило название скин-эффекта.

Пренебрегая данным эффектом, будет справедливым утверждение, что конфигурация магнитного поля не зависима от времени и такая же, как в стационарном режиме. В таком случае время влияет лишь на амплитуду магнитного поля. Этот режим получил название квазистационарного.

Не нашли то, что искали?

Попробуйте обратиться за помощью к преподавателям

Тип работы Выберите тип работыКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

У импульсного соленоида есть характерные свойства: длительность и форма импульса магнитного поля.
Данные параметры зависят от импеданса и конструкции соленоида и источника тока.

Длительность и форму импульса определяют индуктивность, емкость и сумма сопротивлений всех составляющих цепи.

Источники тока и соленоиды рассчитывают одновременно.
Чтобы запитать импульсные соленоиды применяют генераторы переменного тока и батареи электроконденсаторов.

Принципиальная схема создания импульсного магнитного поля

Принципиальная схема генерирования импульсного магнитного поля приведена на рисунке, разберем ее. 

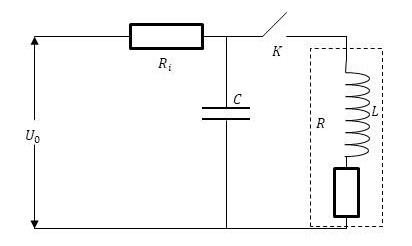
Рассмотрим, что происходит в этой цепи:
Конденсатор заряжается до неизменного напряжения \(U_0\) от источника сквозь сопротивление \(R_i\).
Заряженный конденсатор замыкается на соленоиде. В данном варианте энергия, поглощенная конденсатором, рассчитывается по формуле:

 
\(W_c={(CU^2)\over2} \) (1).

Она преобразуется в энергию соленоида:

\(W_L={LI^2 \over 2}\) (2).

При этом \(W_c≈W_L\).
Рассчитаем энергию, необходимую для запаса в конденсаторе для генерирования магнитного поля, при условии, что оно будет однородным с индукцией \(B_0\):

\(W_c≈{(B_0^2)\over(2μ_0 )} Sl \) (3).

где \( S= {(πd^2)\over4} \), \(d\) – диаметр катушки, \(l \)– длина катушки.
Для правильности расчетов нужно учесть, что поле катушки конечной длины неоднородно. В таком случае магнитную индукцию определяют по формуле:

\(B_0=μ_0 nI_0 cos⁡{d\over l} \) (4).

где \(n\) – число витков катушки, \(I_0\) – сила тока катушки.
Магнитное поле создают с помощью тока импульсного разряда конденсатора \(C\) соленоида без сердечника. Для сердечника индуктивность равна \(L\), а сопротивление \(R\), которое маленькое по величине.
Для того, чтобы взять во внимание потери энергии при прохождении через активное сопротивление \(R\), разберем формулу для собственных колебаний контура\( LCR\):

\(LQ ̈+RQ ̇+ {Q\over C}=0 \) (5).

где \(Q\) – моментальный заряд на конденсаторе. Начало колебания – это момент полного заряда конденсатора при отсутствии тока в контуре:

\(Q(t=0)=U_0 C;I(t=0)={dQ\over dt}=0. \)

При данных базовых условиях выражение (5) будет иметь следующее решение:

\(Q(t)=U_0 C {ω_0 \over ω} e^(-δt) cos⁡(ωt-φ) \) (6),

где \(ω_0^2={1\over LC} \); \(ω={2π\over T} \); \(ω^2=ω_0^2-δ^2 \);\(δ={R \over 2L} \);
\(Z=√{L\over C} \) – сопротивление волны контура; \(tgφ={δ\overω} \).
Из формулы (6) выведем уравнение силы тока в катушке соленоида при \(t'={T \over 4}- {φ \over ω} \) (8).

\(I_m=I(t' )={U_0\over Z} e(-δt' )\) (9).

Таким образом, коэффициент преобразования накапливаемой в конденсаторе энергии в энергию магнитного поля будет определяться по формуле:

\(η={W_L\over W_C} =e^(-2δt' ) \) (10).

При мизерном затухании, с использованием линейной аппроксимации для выражения (10), а также учитывая, что в данном варианте \({φ \over ω}≪{T\over4 }\) и \(ω≈ω_0\), уравнение будет выглядеть так:

\(η≈1--2δt'=1-2δ {T\over4}≈1-{π\over2}  {R\over Z} \) (11).

Формула (11) указывает на то, что для эффективной трансформации в энергию магнитного поля из энергии электростатического будет иметь место такое неравенство:

\(R≪Z\) (12).

В данном варианте потери энергии на нагревание обмотки катушки за период времени t^' очень незначительны. Но в случае продолжительных колебаний практически вся электрическая энергия преобразуется в тепловую. Поэтому, нужно обязательно брать во внимание омическое нагревание катушки соленоида. Именно это явление ограничивает значение энергии накопления, а также предельную величину магнитной индукции.

Применение импульсных магнитных полей

Идея сгенерировать импульсное магнитное поле впервые была озвучена П. Л. Капицей в 1923 году. Он смог создать такое поле величиной 500 килоэрстед, а также подробно изучил процессы в магнитном поле напряженностью до 320 килоэрстед.

Впервые импульсное магнитное поле со значением 2,5*107 А/м получил П. Л. Капица при помощи устройства из кислотных свинцовых аккумуляторов и генератора. В качестве обмотки катушки он использовал кадмиевую медь.

Сложно разобраться самому?

Попробуйте обратиться за помощью к преподавателям

Тип задания Выберите тип заданияКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Сегодня существуют приборы, способные создавать магнитные поля со значением напряженности 8*107 А/м.
Для того, чтобы сгенерировать магнитное поле величиной 4*107 А/м обмотки катушки составляют из металлических дисков с изолирующими прокладками из слюды. Его располагают в пластмассовом корпусе, закрепленном в дюралевом кожухе, имеющем радиально расположенные надрезы. Соленоид охлаждают с помощью жидкого азота. Длина обмотки катушки 10 мм, внутренний диаметр 4,5 мм. Магнитное поле с однородностью 5% создается в цилиндре диаметром 2,5 мм с высотой 3 мм.

Если рассмотреть биттеровский импульсный соленоид, то в нем обмотка сделана в виде спирали из бериллиевой бронзы, помещенной в керамический кожух. Спирали изолируются слюдяными кольцами, имеющими радиальные надрезы. Спирали спаивают с торцевыми латунными пластинами и стягивают шпильками, изготовленными из фосфористой бронзы. Запитывается соленоид от батареи емкостью 2000 мкФ, рабочее напряжение которой 3 кВ. Такая катушка выдает магнитное поле с максимальной напряженностью 6*107 А/м.