1. Общие понятия
2. Суть метода трапеций
3. Погрешность применения метода трапеций

Общие понятия

Методом трапеций является такой метод приближенного интегрирования, который применяют тогда, когда невозможно вычислить первообразную функции и определить с ее помощью интеграл.

Метод трапеций не является единственным методом приближенного интегрирования, на ряду с ним есть и другие, к примеру, метод средних прямоугольников и метод парабол.

Метод трапеций очень схож с методом средних прямоугольников, но считается не таким точным.

Суть метода трапеций

Допустим, необходимо рассчитать интеграл функции \(f(x)\) в интервале \([a;b]\).
Разделим график кривой функции на элементарные сегменты при помощи точек с абсциссами x_i, соединив точки \((x_i,y_i)\), получаем ломаную кривую, причем \(y_i=f(x_i)\), \(i \)может принимать значения от \(0\) до \(n-1\).

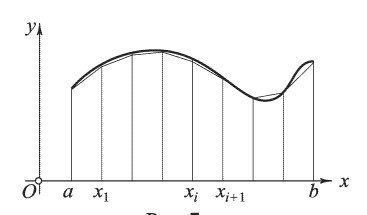
Выбираем число отрезков, на которые разобьём заданный интервал, и вычислим длину каждого такого отрезка по формуле:

\(∆x={b-a\over n}.\)

При расчетах методом трапеций соединяем одну с другой соседние точки разбивки, в итоге образовываются отдельные сегменты. Таким образом, значение функции f(x) берем на границах каждого отрезка.

Вычисляем площадь каждой элементарной трапеции по формуле:

\(S_i={b-a\over n}∙{y_{i-1}-y_i\over 2},\)

Приближенную площадь фигуры, которая ограничена линиями \(x=a,x=b\), осью \(0x\) и графиком кривой \(f(x)\), рассчитаем как сумму площадей всех элементарных сегментов по формуле:

\(∫_a^bf(x)dx≈{b-a\over n}∙({y_0-y_n\over2}+y_1+y_2+⋯+y_{n-1}).\)

Запишем общую формулу приближенного расчета интеграла методом трапеций:

\(∫_a^bf(x)dx≈{x_{i-1}-x_i\over2}∙(f(x_0 )+2∑_{i=1}^{n-1}f(x_i )+f(x_n ) )\)

Погрешность применения метода трапеций

Погрешность применения метода трапеций рассчитывается по формуле:

\(|δ_n |≤max_{x∈[a;b] }\) \(|f'' (x)|\)\(∙n∙{{{(x_i-x_{i-1})\over 2}^3}\over 12}\)\(=max_{x∈[a;b] }\) \(|f'' (x)|∙\)\({n∙(b-a)^3\over12n^2 }\).

Данный метод удобнее всего применять, когда сама функция \(f(x)\) не задана, но заданы значения, которые она принимает в точках разбивки. Если график задан, то вычисления проще и точнее проводить при помощи метода средних прямоугольников.

Не нашли то, что искали?

Попробуйте обратиться за помощью к преподавателям

Тип работы Выберите тип работыКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Если нет возможности рассчитать максимум функции, то вычислить погрешность будет сложно. При таких условиях делают следующие действия: вначале проводят численное интегрирование методом трапеций при \(n=10\), далее в этом же интервале проводят интегрирование при \(n=20\).

Рассчитывают разность найденных значений, если она меньше требуемой погрешности, то в ответ записывают значение интеграла при \(n=20\), на этом расчет считается оконченным. Если же найденная разность выше необходимой погрешности, расчеты продолжают, каждый раз удваивая число отрезков, пока не достигнут нужной точности.

Рассмотрим пример решения подобной задачи.
Задача 1. Вычислить интеграл \(∫_1^2{dx\over x}=ln⁡2 \) с точностью до 0,001 методом трапеций.
Порядок решения:
1) Разбиваем заданную функцию на 10 равных отрезков.
2) Оцениваем погрешность расчетов:

\(|δ_n |≤max_{x∈[1;2] }\) \(\begin{vmatrix} \left(\frac{x}{1}\right) \end{vmatrix}'' \)\(∙{n∙(2-1)^3\over 12∙10^2}=0.00008\),

то есть погрешность при \(n=10\) меньше заданной, это означает, что для расчета достаточно разбить отрезок на 10 сегментов.
3) Длина каждого сегмента будет равна:

\(∆x={2-1\over10}=0,1.\)

4)Рассчитываем значение функции для границ каждого отрезка:
\(x_0=1,0; y_0=1,0000;\\ x_1=1,1; y_1=0,9091;\\ x_2=1,2; y_2=0,8333;\\ x_3=1,3; y_3=0,7692;\\ x_4=1,4; y_4=0,7143;\\ x_5=1,5; y_5=0,6667;\\ x_6=1,6; y_6=0,6250;\\ x_7=1,7; y_7=0,5882;\\ x_8=1,8; y_8=0,5556;\\ x_9=1,9; y_9=0,5263;\\ x_10=2,0; y_10=0,5000.\)
  
5) Рассчитываем сумму найденных значений, она равна 6,1877.

Сложно разобраться самому?

Попробуйте обратиться за помощью к преподавателям

Тип задания Выберите тип заданияКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

6) Таким образом, значение интеграла будет равно:

\(∫_1^2{dx\over x}=0,1∙({1,5000\over2})+6,1877=0,69377.\)

Найденное значение интеграла соответствует необходимой точности.