Бесконечно малые величины и их свойства

1. Основные понятия о бесконечно малых величинах
2. Исчисление бесконечно малых величин

Основные понятия о бесконечно малых величинах

Суть бесконечно малых величин очень тесно переплетается с сутью пределов.

Бесконечно малые величины – это такие числовые функции либо последовательности, которые стремятся бесконечно к нулевому значению.

Рассмотрим бесконечно малые величины по графикам. На первом рисунке функция \(y=f(x)\) пересекается с осью \(0x\). На втором – прикасается к оси \(0x\) в точке \(x=a\).

Исчисление бесконечно малых величин

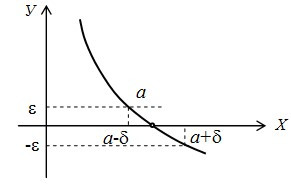
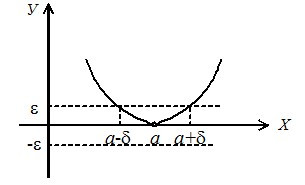
Исчисление бесконечно малой величины – это процесс вычисления, связанный с бесконечно малыми величинами, в результате него получают бесконечно непрерывные суммы бесконечно малых величин.

Бесконечно малой последовательностью есть такая последовательность \(a_n\), для которой справедливо выражение:

\(\lim\limits_{x \to \infty} \ a_n =0.\)

Данная последовательность бесконечно уменьшается, а соответственно, она представляет собой бесконечно малую величину.

Не нашли то, что искали?

Попробуйте обратиться за помощью к преподавателям

Тип работы Выберите тип работыКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Функция будет бесконечно малой величиной в бесконечном множестве в том случае, когда будет справедливо одно из равенств:

\(\lim\limits_{x \to \infty} f(x)=0; \lim\limits_{x \to \infty} ⁡f(x)=0.\)

Функция будет бесконечно малой величиной в около точки \(x_0\) в том случае, когда будет справедливо равенство:

\(\lim\limits_{x \to \infty}f(x)=0.\)

Бесконечно малая величина переменна, причем если x стремится к \(a\), она всегда меньше, чем число ε:

\(\lim\limits_{x \to \infty}f(x)=0.\)

Функция \(y=f(x)\)) будет бесконечно малой при \(x>+∞\), когда при любом значении \(ε>0\) существует число \(N\), при котором \(x>N\) справедливо условие:

\(f(x)={1\over x^a} . \)

Рассмотрим доказательство того, что функция \(y={1\over x^2} \)  будет бесконечно малой, при условии, что \(x>+∞\).
Для начала определимся, что пределом для функции при \(x>+∞\) будет \(b=0\), то есть для любого числа \(ε>0\) существует некое число \(N\), при котором \(x>N\) и выполняется условие:

\( |f(x)|=|{1\over x^2 }|={1\over x^2} . \)

Это неравенство выполняется только при \(x>{1\over\sqrt{ε}}=N \).

Соответственно по аналогии для функции \(y={1\over x^a}\)  , где \(a\) является некоторым положительным числом.

Таким образом, будет верным вывод, что функция будет бесконечно малой.

Бесконечно малой считается также функция, которая есть разницей между функцией и ее пределом, это выглядит следующим образом:

\(\lim\limits_{x \to \infty}f(x)=a, то f(x)-a=a(x),   \lim\limits_{x \to \infty}⁡(f(x)-a)=0.\)

Рассмотрим функцию \(y=2-{1\over x}\). Будет ли она бесконечно малой при \(x>+∞\).

\(\lim\limits_{x \to \infty}⁡ (2-{1\over x})=2-0=2≠0.\)

А это означает, что заданная функция\( y=2-{1\over x}\) при \(x>+∞\) не будет бесконечно малой.

Сложно разобраться самому?

Попробуйте обратиться за помощью к преподавателям

Тип задания Выберите тип заданияКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Рассмотрим еще одно доказательство. Дана функция \(y=x^3\) и доказательство того, что она будет бесконечно малой при \(x>0\).

Допустим \(ε>0\). Неравенство \(|f(x)|=|x^3 |\). Соответственно \(N=-∛ε\) и \(M=∛ε\).
А это обозначает, что \(\lim\limits_{x \to \infty} x^3=0\), иными словами, заданная функция \(y=x^3\) будет бесконечно малой при \(x>0\).

Рассмотрим еще один пример с доказательством. Допустим дана функция \(y={1\over x}+{1\over√x}+{1\over x^2}\) . Будет ли она бесконечно малой при \(x>+∞\).

Каждое слагаемое по отдельности представляет собой бесконечно малую функцию при \(x>+∞\), потому в соответствии со свойством бесконечно малых функций, их сумма тоже будет бесконечно малой величиной.