Определение параллельных прямых в пространстве

1. Понятие о параллельных прямых
2.  Теоремы о параллельности двух прямых
3. Свойства параллельных прямых в пространстве
4. Пример задачи о параллельных прямых

Понятие о параллельных прямых

Прямые \(a\) и \(b\) являются параллельными в трехмерном пространстве только в том случае, если они находятся в одной плоскости и не пересекаются.

Если рассмотреть примеры, то параллельные прямые мы можем наблюдать как противоположные края у прямоугольного или квадратного стола, железнодорожные рельсы и шпалы, провода линий электропередач, линии в тетради в полоску и прочее. Таких примеров из реального мира можно привести очень много.

Другими вариантами прямых, расположенных в 3D-пространстве, есть их скрещивание и пересечение. Пересекающимися есть прямые, имеющие общую точку, она же и есть точкой пересечения. Скрещивающимися есть прямые, расположенные в разных плоскостях и не параллельные между собой.

Есть ряд теорем, описывающих поведение параллельных прямых в пространстве. Рассмотрим их подробнее.

Теоремы о параллельности двух прямых

Теоремы: 

1. если две прямые в пространстве перпендикулярные к одной плоскости, то они параллельные между собой;
2. через точку в пространстве, что не расположена на заданной прямой, возможно провести лишь одну прямую, параллельную заданной.

Доказательство теоремы: Через прямую a и точку \(M\), не находящуюся на данной прямой, проведем плоскость ∝. Эта плоскость определяется заданной прямой a и точкой \(M\), то есть она однозначно определена.

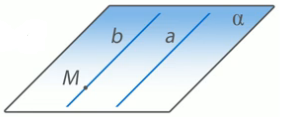
Для доказательства этой теоремы применим евклидовую аксиому из планиметрии про параллельные прямые.
Таким образом, через точку \(M\) возможно проложить лишь одну прямую, параллельную прямой \(a\), и ее существование доказано. Назовем эту прямую \(b\).
Два отрезка будут параллельными при их расположении на параллельных прямых.

Свойства параллельных прямых в пространстве

Некоторые свойства пересекаются с вышеизложенными теоремами, но все же рассмотрим их все:

1. имея две параллельных прямых, одна из которых параллельная третьей прямой, можно утверждать, что вторая тоже будет параллельна третьей;
2. если из двух параллельных прямых одна пересекает некую плоскость, то и вторая так же будет ее пересекать. Это свойство является леммой про две параллельные прямые в пространстве, ее применяют при обоснованиях различных геометрических теорем;
3. при помощи двух параллельных прямых можно изобразить однозначно заданную плоскость;
4. через любую точку, находящуюся в 3D-пространстве и не расположенную на заданной прямой, возможно провести лишь одну прямую, что параллельна заданной.

Рассмотрим подробнее лемму про параллельные прямые и докажем ее. К примеру, некая прямая \(b\) пересекает плоскость \(∝\) в точке \(M\), что расположена на заданной плоскости. Параллельные прямые a и образуют некую плоскость \(β\). Таким образом, если точка \(M\) общая для плоскостей \(∝\) и \(β\), то эти плоскости пересекаются, линию пересечения обозначим c, на ней расположена точка \(M\).
Все прямые \(a\), \(b\) и \(c\) расположены в плоскости \(β\).

Не нашли то, что искали?

Попробуйте обратиться за помощью к преподавателям

Тип работы Выберите тип работыКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

В соответствии с аксиомой планиметрии, при пересечении одной из параллельных прямых третьей прямой, вторая так же будет ее пересекать.

В нашем варианте прямая a пересекает прямую c в точке \(K\). 

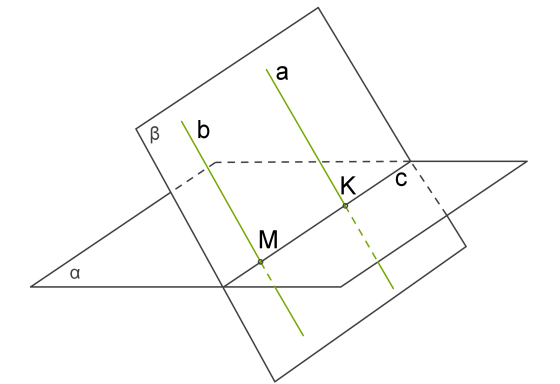
Точка \(K\) расположена одновременно на прямой a и на плоскости \(∝\), значит она есть общей для них. Таким образом, прямая a пересекает плоскость \(∝\).

Пример задачи о параллельных прямых

Заданы прямые \(a\) и \(b\), описывающиеся уравнениями. Определить, параллельны ли заданные прямые.
\(a: {(x-1)\over 1}={(y-1)\over 3}={(z+1)\over (-2)} \);

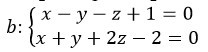
При совпадении прямых или если они параллельны их направляющие векторы \(s_1\) и \( s_2\) будут коллинеарными, таким образом, их координаты будут иметь следующее соотношение:

\({x_1\over x_2} ={y_1\over y_2} ={z_1\over z_2} .\)

Для того, чтобы найти направляющие вектора, воспользуемся каноническими уравнениями, таким образом для прямой a вектор \(s_1\) будет равен {1;3;-2}.

Для прямой b найдем направляющий вектор при помощи произведения нормальных векторов плоскостей, на которых он расположен:

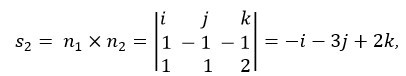
таким образом, \(s_2\)= {-1;-3; - 2}.
\(s_1=-s_2\).

Таким образом, соблюдается вышеуказанное условие, значит эти прямые либо параллельны, либо совпадают. Необходимо определить каковыми именно они являются: параллельны или совпадают. Возьмем некую точку \(K\) с координатами (1;2;-1), находящуюся на прямой a, и подставим ее координаты в уравнение прямой \(b\):
1-2+1+1=0;1=0,

Равенство не выполняется, таким образом, точка \(K\) не расположена на прямой \(b\), а это означает, что прямые \(a\) и \(b\) не совпадают, соответственно они параллельны.