Законы силы, формулы

1. Закон силы тяжести
2. Законы сил трения
3. Закон силы упругости

Рассмотрим законы, описывающие процессы, что происходят при механических движениях объектов. К этим законам относятся:

• закон силы тяжести;
• закон всемирного притяжения;
• законы Ньютона;
• законы сил трения;
• закон силы упругости.

Закон силы тяжести

Силой тяжести есть такая сила, которая воздействует на тела с массой, пребывающие вблизи планет, и наделяет их ускорением свободного падения. Формула для расчета ускорения свободного падения имеет следующий вид:

\(g=G {M \over r^2 } ,\)

где \(G \)– гравитационная постоянная, G=6,7∙10^-11 Н∙м²/кг²;

       \(M\) – масса планеты или другого космического тела;

       \(r\) – расстояние между объектом и планетой.

Сила тяжести рассчитывается по такой формуле:

\(\overrightarrow{F_g} = m\overrightarrow{g}.\)

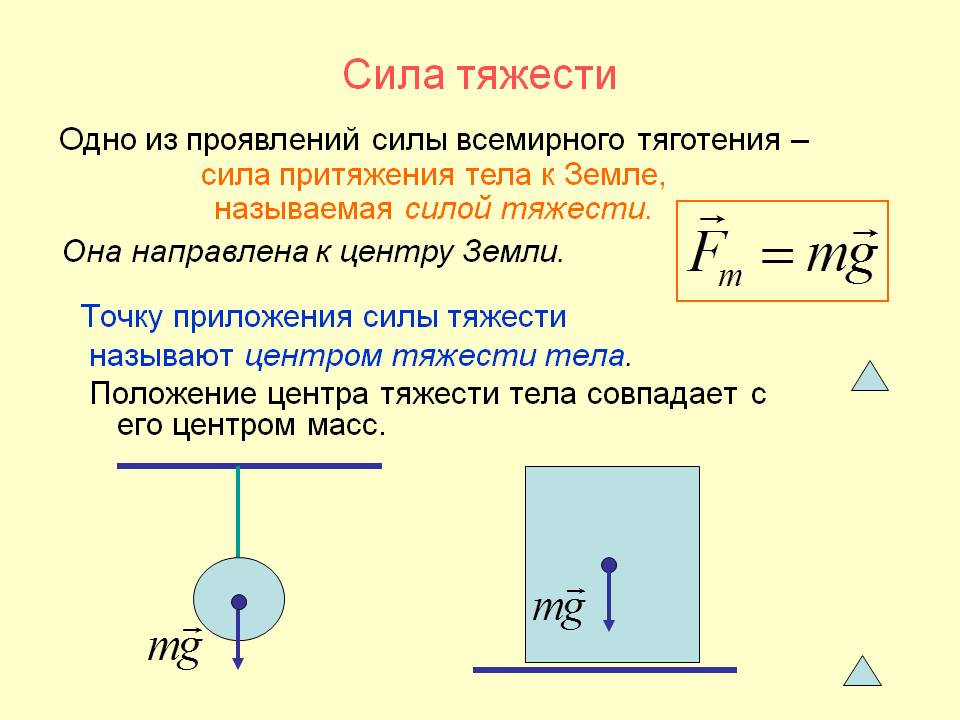
Сила тяжести – векторная величина, то есть ей присуще определенное направление действия, а именно к центру планеты или иного небесного тела. Так как вблизи планеты данная сила действует постоянно, объект свободно падает с постоянным ускорением. При этом траектория движения под воздействием силы тяжести зависима от нескольких параметров:

• направления вектора скорости;
• модульного значения начальной скорости.

С воздействием силы тяжести в повседневной жизни мы сталкиваемся на каждом шагу. Эту силу часто путают с весом тела, так как формула их расчета одинакова:

\(P=mg,\)

но физический смысл этих сил различный. Сила веса возникает под воздействием силы тяжести, но ее суть в том, что она характеризует силу действия объекта на опору, в отличие от силы тяжести, действующей на объект.

Не нашли то, что искали?

Попробуйте обратиться за помощью к преподавателям

Тип работы Выберите тип работыКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Если мы рассмотрим закон всемирного притяжения, сформулированный Исааком Ньютоном, то он гласит о том, что все тела, имеющие определенную массу, притягиваются друг к другу под воздействием силы гравитации:

\(F=G {m_1 m_2 \over r^2}.\)

Если объект движется с равномерной скоростью по горизонтальной плоскости или находится в состоянии покоя, возникает сила реакции опоры, которая по значению будет равняться весу тела:

\(P=τg.\)

При этом она будет также равняться силе тяжести.

Если же объект движется равноускоренно вдоль вертикали, его вес не будет равняться по значению силе тяжести. Его значение будет зависеть от направления вектора ускорения. Если он направлен противоположно действию силы тяжести, объект находится в состоянии перегрузки. Если же объект движется вниз и при этом \(a=g\), вес приравнивается к нулю, а объект находится в невесомости.

Напряженность тяготения гравитационного поля определяют по формуле:

\(g= {F \over m},\)

где \(F\) – сила тяжести, воздействующая на материальную точку с массой m.

Потенциальная энергия гравитационного взаимодействия двух материальных точек с массами \(m_1 \) и  \(m_2, \)находящихся на расстоянии \(r\) рассчитывается так:

\(E_p=Gm_1 m_2 r.\)

Законы сил трения

Различают силы трения скольжение, качения, внешнего трения, вязкого трения и прочие. При этом выделяют силу статического трения, которая имеет место в стационарном состоянии тела, прямо пропорциональна силе нормальной реакции и не зависима от размеров тела и состояния трущихся поверхностей.

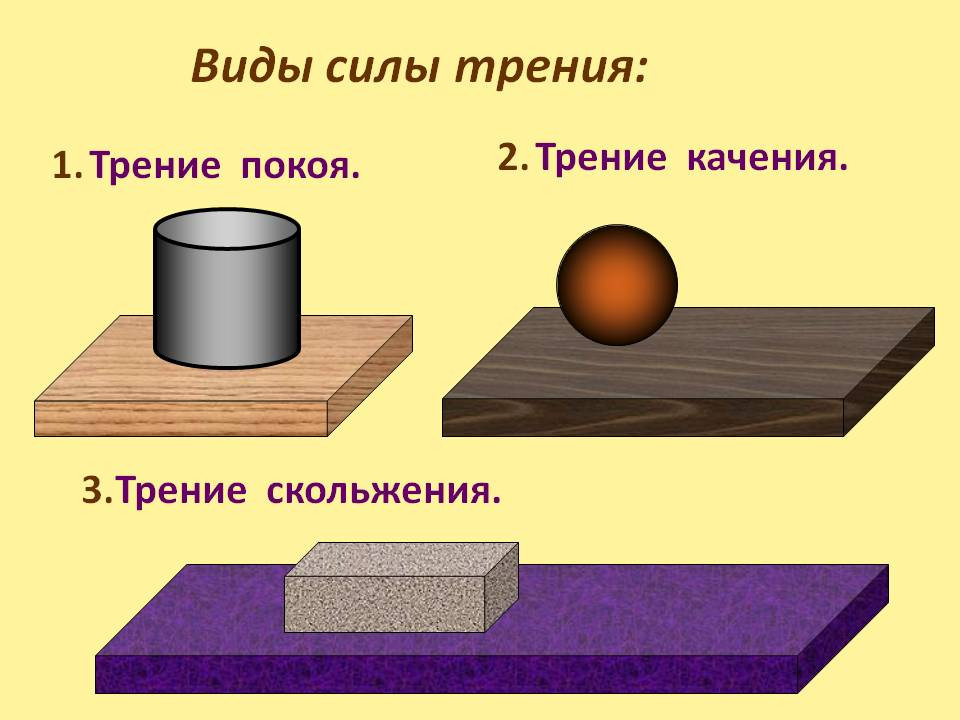
Материал соприкасающихся тел и состояние их поверхностей влияет на статический коэффициент трения. При этом силы трения не стабильны, так как состояние поверхности не однородно.

Сложно разобраться самому?

Попробуйте обратиться за помощью к преподавателям

Тип задания Выберите тип заданияКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин. языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое

Предмет

E-mail

Узнать стоимость

это быстро и бесплатно

Традиционная формула расчета силы трения:

\(F=ηN,\)

где \(η\) – коэффициент трения;

      \(N\) – сила нормального давления.

Закон силы упругости

Сила упругости зависима от жесткости тела и степени его деформации:

\(F=k∙∆l,\)

где \(k \)– коэффициент жесткости тела;

       \(∆l\) – величина деформации.

Сила упругости, как и любая другая сила, измеряется в Ньютонах (Н).

Данная формула является описанием закона Гука. Его суть состоит в том, что при любой деформации тело стремиться принять первоначальное состояние при помощи силы упругости.

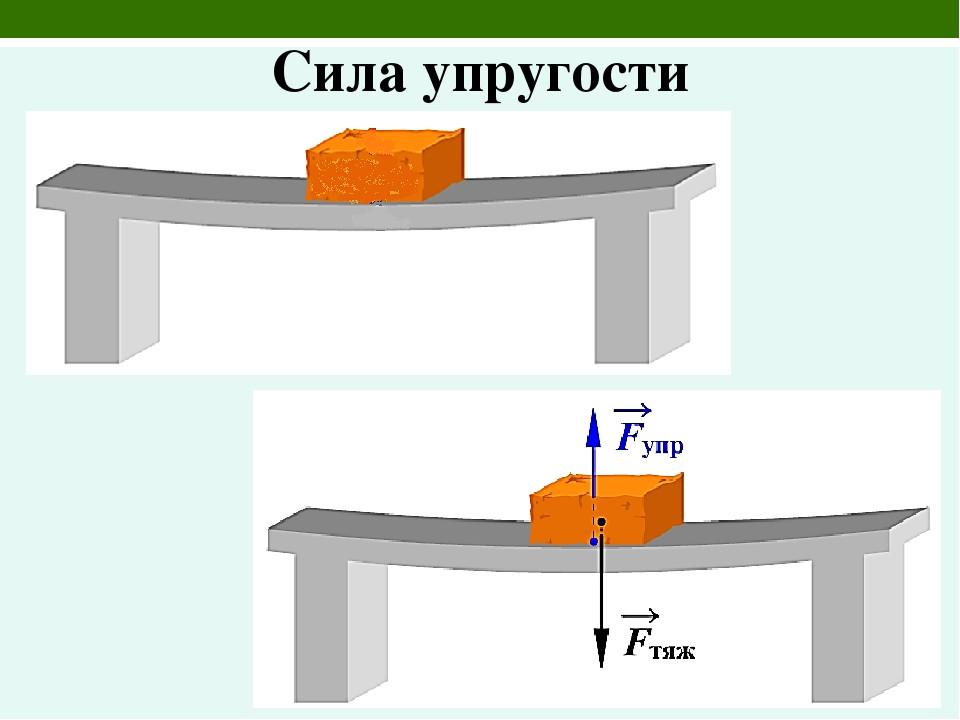
Коэффициент упругости в каждом случае будет применяться разный, так как он зависит от материала изготовления объекта деформации и его размеров. Рассчитывается он по следующей формуле:

\(k= {ES \over L},\)

где \(E\) – модуль упругости первого рода или модуль Юнга. Зависит от механических параметров материала;

      \(L\) – длина стержня;

      \(S\) – площадь его поперечного сечения.

В процессе расчета прямого стержня используют такую запись закона упругости Гука:

\(∆l= {FL\over ES}.\)

Стоит отметить, что закон Гука применим лишь при незначительных деформациях. При возрастании деформаций после определенного момента взаимосвязь деформации с напряжением становится нелинейной. А в некоторых средах закон Гука и вовсе не применим.